コンデンサー

金属の板を向い合せに置き、それぞれに電池をつなぐと、一方には正電荷、他方には負電荷がたまっていき、電荷を蓄えることができる。このようにして電気を蓄える装置をコンデンサーという。
コンデンサー
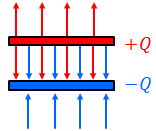
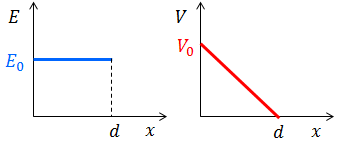
一方の金属板の電気量が+Q〔C〕、もう一方が-Q〔C〕であるとき、周囲の電場は図のようになっている。このとき、コンデンサーは「Q〔C〕の電気量を蓄えている」という。
このとき、一方の金属板が作る電場の大きさは、金属板の面積をS〔m2〕として、以前の問題の解答より、

であるから、2つの金属板に挟まれた領域における電場の大きさE〔N/C〕はその2倍となり、
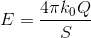
であると分かる。

また、金属板の間隔d〔m〕, 電位差V〔V〕を使って電場E〔V/m〕を表すと、
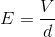
であるから、上の式と合わせることで
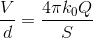
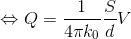
という関係が導ける。ここで、
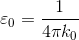
とおけば、
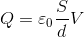
となるので、さらに
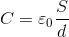
とおけば、
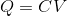
となる。この式はコンデンサーに関係する式の中で1番重要なので、これを「コンデンサーの公式」と呼ぶことにしよう。
また、Cを電気容量(静電容量)といい、単位は〔F〕(ファラド)。電気容量には、定義を見ても分かるように、
- 金属板の面積Sが大きいほど大きい(比例)
- 金属板の間隔dが狭いほど大きい(反比例)
という性質がある。これは、蓄えることのできる電気量の大きさを表している。
静電エネルギー
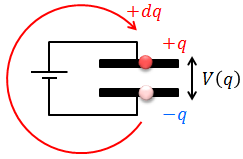
続いて、Q〔C〕の電気量を蓄えたコンデンサーが持つエネルギーU〔J〕を求めてみよう。コンデンサーがq〔C〕の電気量を蓄えているとき、電位差Vは、コンデンサーの公式より、

である。
このとき、負の電荷を持っている極板側から、+dq〔C〕の微小な電気量を持った電荷をもう一方の極板へ移動させるときの微小な仕事dWは、
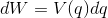
だから、これをq=0の状態からq=Qの状態になるまで足し合わせることで、全体の仕事Wを求めることができる。

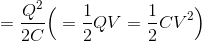
( )の中は、コンデンサーの公式を利用した。
電荷の移動が終了したとき、このコンデンサーはWと同じ大きさのエネルギーを蓄えていることになるから、
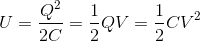
である。これを静電エネルギーという。
誘電体

コンデンサーがQ〔C〕の電気量を蓄えているとき、極板間につくられる電場Eと電位差Vを、位置xを横軸としてグラフ化してみると、以下のようになる。
電場Eは一定である。電位差Vは、負に帯電した側を基準(φ=0)とすると、右肩下がりのグラフとなる。
それでは、上の状態に続いて、電池をコンデンサーから切り離した状態で極板間を不導体(絶縁体)で満たしてみよう。コンデンサーを考えるときには、挿入した不導体のことを誘電体と呼ぶことが多い。
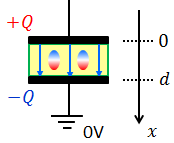
誘電体を挿入すると、不導体の内部で誘電分極が起こり、極板間の電場は弱まる(E0→E)。この結果、極板間の電位差Vも小さくなる(V0→V)。
コンデンサーを電池から切り離している場合、コンデンサーが蓄えている電気量Qは変化しない。この状況で電位差Vが小さくなったということは、コンデンサーの公式「Q=CV」より、電気容量Cが大きくなったと考えることができる。
ここで、誘電体で内部を満たす前のコンデンサーの電気容量が
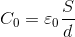
だったから、内部を誘電体で満たした後の電気容量を、
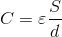
と表すことにする。このとき、εは誘電体の分極のしやすさを表す量で、誘電率という。また、それらと比較したときの真空における値ε0を、真空の誘電率という。

また、
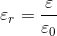
を比誘電率というので、これを使って電気容量Cを表すと、
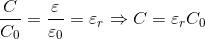
となり、電位差Vは
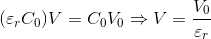
となる。
まとめると、電池をコンデンサーから切り離している場合、
- Qは不変
- Cは増える(εr倍)
- Vは減る(1/εr倍)

それでは、コンデンサーを電池につないだまま、誘電体を挿入した場合を考えてみよう。このとき、コンデンサーの極板間の電位差は変わらない。また、誘電体を挿入すると電気容量は増えるので、コンデンサーの公式「Q=CV」より、蓄えている電気量Qは増加することが分かる。
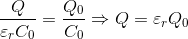
まとめると、電池をコンデンサーにつないでいる場合、
- Vは不変
- Cは増える(εr倍)
- Qも増える(εr倍)
