直流回路Ⅱ
電池と抵抗からなる直流回路なら、多少複雑な問題でも「電流の式」と「電位の式」を立てることによって解くことができる。今回はオームの法則に従わない抵抗やコンデンサーを含む回路について学ぶが、基本的なことは前回と変わらない。
非オーム抵抗を含む回路
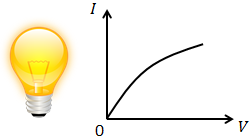
電圧と電流の関係がオームの法則「V=RI」に従わない抵抗を非オーム抵抗(非直線抵抗)と呼ぶ。電圧を上げていくことによって抵抗の熱運動が激しくなり、抵抗が大きくなるためだ。
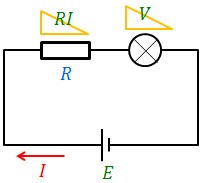
図のような回路を考えて、非オーム抵抗の前後の電位差と流れる電流を求めてみよう。〇の中に×が書いてある記号が非オーム抵抗である。この抵抗の前後の電位差をV、オーム抵抗の前後の電位差をRI、電池の起電力をEとすると、キルヒホッフの第2法則より、次のような「電位の式」を立てることができる。

この式より、回路を流れる電流Iは

という形で書けることが分かるから、

この結果を非オーム抵抗の特性を表すグラフに描き入れる。このグラフの交点が答えである。
なぜこれでよいのかというと、2つのグラフの交点を読み取るという行動は、連立方程式を解くことと同じだからだ。
コンデンサーを含む回路

次はコンデンサーC1,C2とスイッチS、電池Eからなる図のような回路を考える。はじめ、コンデンサーには電気量は蓄えられていないものとする。

それでは、スイッチを入れて十分に時間が経過した後、コンデンサーC1,C2が蓄えている電気量Q1,Q2を求めてみよう。
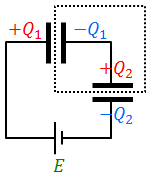
まずは回路上の孤立した部分に注目する。スイッチSを閉じる前と後とで電気量は変わらないはずだから、

という関係が成り立っている。これを電気量保存則という。

続いてコンデンサーC1,C2の電圧V1,V2をそれぞれ求める。コンデンサーの公式「Q=CV」より、

と計算することができる。するとキルヒホッフの第2法則から「電位の式」を作ることができて、
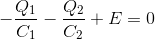
この式と電気量保存則の式から、Q1,Q2が求められる。
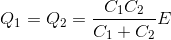
抵抗のみからなる直流回路の場合は、キルヒホッフの第1法則を使って「電流の式」を作ったが、コンデンサーを含む直流回路の場合は、「電流の式」の代わりに「電気量保存則の式」を立てればOKというわけだ。
コンデンサーと抵抗を含む回路
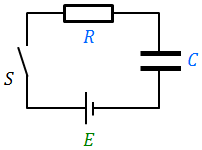
次は、抵抗RとコンデンサーCを図のように直列につないだ回路を考えてみよう。このような回路の場合、「スイッチを閉じた直後」と「十分に時間が経過した後」に分けて考える必要がある。

スイッチを入れた直後、コンデンサーに電気量が蓄えられていないとすれば、コンデンサーには電位差がないということになる。
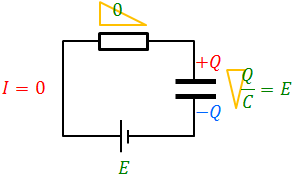
その後、徐々にコンデンサーに電気量が蓄えられていき、電位差が表れていく。そして、十分に時間が経過すると、コンデンサーの電位差Q/Cが電池の起電力Eと等しくなって充電が完了する。このとき、抵抗には電位差がないので、電流は流れない。
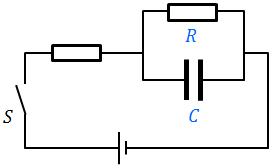
以上のことを踏まえて、抵抗RとコンデンサーCが並列につながれた図のような回路について説明しておく。

まずスイッチを入れた直後は、コンデンサーCに電気量が蓄えられていないので、Cの電位差は0。だから、抵抗Rの電位差も0ということになり、抵抗に電流は流れない。
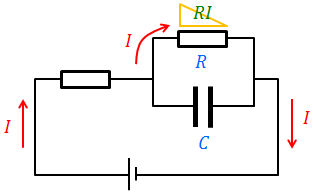
その後、徐々にコンデンサーCに電気量が蓄えられていくと、抵抗R側にも電流が流れるようになる。十分に時間が経過した後、コンデンサーの充電が完了するとコンデンサー側に電流が流れなくなるので、電流はすべて抵抗を通過することになる。このとき、
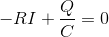
という「電位の式」が成り立っている。
