ガウスの発散定理

ベクトルEを「∇・E」と微分したものを「div E」と表し、これが正のときは微小領域からEが湧き出していることを意味している。
ガウスの発散定理

「div E」は”単位体積あたりの”流出量を表しているので、微小体積dVからの流出量は、

と表される。これを、体積Vの大きな領域に含まれる微小体積すべてで計算して足し合わせることを、
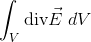
と表す。この意味についてよく考えてみよう。
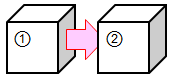
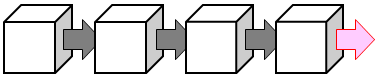
いま、微小領域①からベクトルEが流出して、微小領域②へそのまま流入しているだけのとき、②の「流出量」は負になるので、それぞれの領域からの「流出量」の和は0になる。
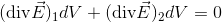
このように、隣り合う領域の流出量と流入量は必ず等しく、打ち消し合うので、大きな領域全体の和を考えるときは、最後の領域の流出量だけを考えればいいことになる。つまり、体積Vの大きな領域の内部はすべて打ち消し合うので、表面から出てくるベクトルだけをイメージすればいいということだ。

ここで、体積V、表面積Sの領域から流出するベクトルEの、表面全体の和は

と書けるから、

という関係が成り立つことになる。これをガウスの発散定理という。ガウスの発散定理は、積分範囲を面積Sと体積Vで変換するための公式だともいえる。
ガウスの法則
ガウスの発散定理の使用例を紹介しよう。
「電気量Qの電荷を内部に持つ閉曲面から放出される電気力線の和は4πkQ本である」。これをガウスの法則といい、

と表される。ここで、この式を真空の誘電率ε0

を思い出せば、

と簡潔に書き直すことができる。ここで、左辺はガウスの発散定理そのものなので、

と変形しておこう。
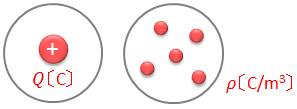
ところで、電荷が領域内に散らばって分布しているとき、ある部分の電荷密度をρ〔C/m3〕とすると、微小体積dV〔m3〕に含まれる電荷の電気量dq〔C〕は、
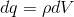
である。この合計がQ〔C〕であるとき、

という式が成り立つ。この関係式を用いてガウスの法則の式を書き変えると、

となる。すると積分範囲が両辺で等しくなるから、

と積分記号を外すことができる。これを「ガウスの法則の微分形」と呼ぶ。
電荷と電流の連続の方程式

電気量+Qに帯電した導体に導線をつなぐと、電流が流れる。このとき、Qの時間変化量が電流Iになることから、

という関係がある。Qは減少していくということに気を付けよう。
ここで、電流Iは電流密度iを用いて
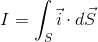
と表されたことを思い出せば、上の式は
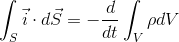
になる。右辺は電荷密度ρを用いてQを表した。さらに、左辺にガウスの発散定理を使えば、
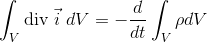
となり、積分記号を外せば、

となる。これを「電荷と電流の連続の方程式」という。
