分極
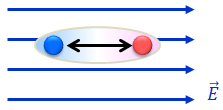
不導体(絶縁体)に帯電体を近づけると、不導体中の原子の電荷バランスが崩れ、誘電分極という現象を起こす。一般的に、電気や磁気に偏りが生じる現象を分極という。磁石は必ずN極とS極がペアとなっているので、常に分極していると考えることができる。
電気分極
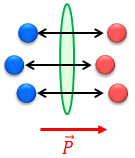
分極によってある面を電荷が通過したとき、単位面積当たりの電気量を大きさに持ち、負電荷から正電荷に向かう向きのベクトルを定め、これを分極ベクトルPと呼ぶことにする。大きさの定義から、単位は〔C/m2〕である。
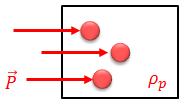
ある領域(体積dV)にベクトルPが流入しているとき、この流入量、つまり分極電荷の電気量は「-div P dV」と表される。また、分極電荷の密度をρ(p)とすると、分極電荷の電気量は「ρ(p)dV」と表せるから、
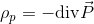
という関係があることがわかる。
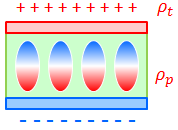
ここからは、分極によって生じる電荷Q(p)とそれ以外の真電荷Q(t)を分けて考えてみよう。真電荷の電荷密度をρ(t)とすると、電荷密度の合計ρは、ρ(t)とρ(p)の和
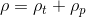
になるから、ガウスの法則の微分形の式は、
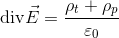
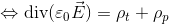
と書き直されることになる。ここで、分極電荷密度ρ(p)と分極ベクトルPの関係式を使えば、
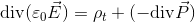

と、変形できる。さらに、
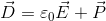
とおくと、
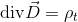
になる。このとき、D〔C/m2〕を電束密度という。
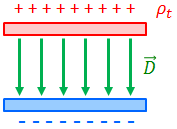
どうやら、電束密度Dというやつの発散(div D)は、真電荷の密度ρ(t)にしか影響を受けないらしい。ということは、誘電体があろうがなかろうが、この値は変わらないということだ。
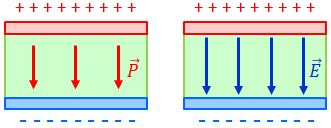
電束密度Dは誘電体の影響を受けないが、電場Eはそうはいかない。電束密度Dの定義式を書き変えると、
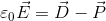
となり、電場Eは電束密度Dから分極Pを引いて定数倍したものだということが分かる。だから、分極Pが大きければ大きいほど、電場Eは小さくなってしまうのだ。
また、分極Pの大きさは、与える電場Eの大きさに比例すると考えられるから、
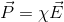
と置くことにしよう。このとき、χを電気感受率という。この式を電束密度の定義式へ代入すると、
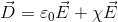
となる。さらに、

とおけば、
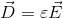
となる。εは誘電体の誘電率である。また、
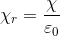
を比電気感受率という。
磁気分極
電気分極と同様に、磁気分極Mを考えよう。
磁石は必ずN極とS極がペアになっていて、片方の磁極を取り出すことができない。つまり、真磁荷というものが存在しないので、分極磁荷密度ρ(m)だけを考えればよい。ρ(m)と磁気分極Mの関係は、

である。この関係を使って磁場に関するガウスの法則の式

を書き変えると、
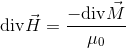
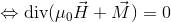
となるから、
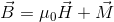
とおく。すると、
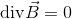
となる。B〔Wb/m2〕を磁束密度という。単位には〔T〕(テスラ)も使う。
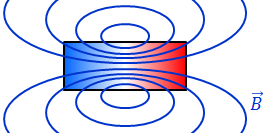
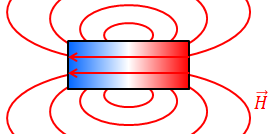
「div B」が0になるということは、真磁荷というものが存在せず、ベクトルBが湧き出す場所がないということを示している。だから、磁束密度Bの矢印(磁束線)は途切れることはない。

さらに、MがHに比例するとき、
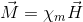
Χ(m)を磁気感受率という。これを磁束密度の式へ代入すると、
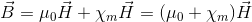
となるので、さらに
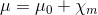
とおけば、
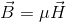
となる。μは磁性体の透磁率と呼ばれる。また、
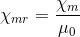
を比磁気感受率という。X(mr)の値が大きな物体を強磁性体(鉄、コバルト、ニッケル)、小さな物体を常磁性体、負の物体を反磁性体という。
