電流が作る磁場

1820年、大学の講義中に演示実験をしていたエルステッドは、電流を流した導線の近くに置いてあった方位磁針が北以外を指していることに気付いた。電流が磁場を作る。この発見により、それまではバラバラであった電気と磁気が結び付けられ、電磁気学の発展へとつながっていく。
右ねじの法則
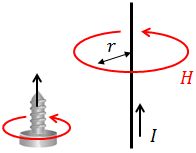
電流の周囲には、電流の向きに進む右ねじが回転する向きに円形の磁場ができる。この法則を右ねじの法則という。
このとき、磁場の半径をr,電流をIとすると磁場の大きさHは、
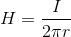
と表される。

右ねじの法則を知っていれば、円形の導線を流れる電流が円の中心に作る磁場の向きもすぐに分かる。電流の向きに回転した右ねじが進む向きに磁場ができるのだ。
このとき、導線の半径をr,電流をIとすると磁場の大きさHは
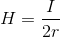
と表される。
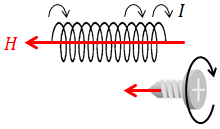
円形電流が作る磁場を知っていれば、ソレノイド(ながーく巻いたコイル)がその内部につくる磁場の向きもすぐに分かる。
また、ソレノイドの1mあたりの巻き数をn,電流をIとすると、磁場の大きさHは、

と表される。
ビオ・サバールの法則

導線の一部dsを流れている電流Iが、位置rにつくる微小な磁場dHは、
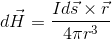
と表される。これをビオ・サバールの法則という。「×」は外積なので、dHはベクトルになっている。
導線を流れる電流全体が、同じ位置につくる磁場Hは、dHを導線全体で足し合わせれば求められるから、
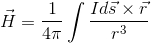
で計算することができる。
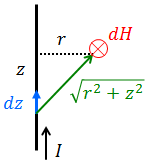
それでは、ビオ・サバールの法則を使って、直線電流が導線からrだけ離れた位置につくる磁場の大きさHを求めてみよう。
まず、導線に沿ってz軸を取り、その一部dzが目的の位置につくる微小な磁場dHを考える。外積の大きさはベクトルの直交成分の積だから、
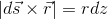
であることに注意すれば、

と表すことができる。これを導線全体について計算するためには、z=-∞~∞の範囲でこれを積分すればいい。
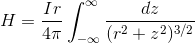
z=r tanθとすると、
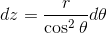
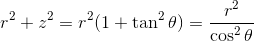
だから、
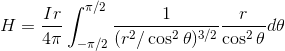
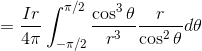
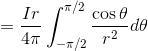
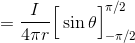
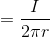
このようにして直線電流がつくる磁場Hを求めることができる。
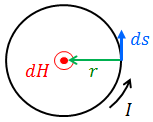
続いて、円形電流がその中心に作る磁場の大きさを求めよう。
まず、導線の一部dsが中心に作る微小な磁場dHは、
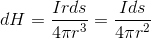
と書けるから、これを導線全体で積分すればいい。
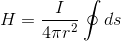
∫dsは導線の長さだから、
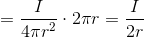
となる。
アンペールの法則
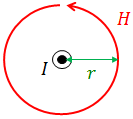
ここで、直線電流がつくる磁場の式を、
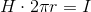
と書き変える。2πrは半径rの円周の長さだから、
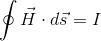
という式を作ることができる。これをアンペールの回路定理と呼ぶ。閉回路に沿って磁場H・dsを足し合わせた結果は、その内部を通過する電流Iに等しいという意味だ。
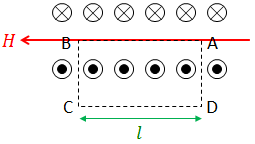
では、アンペールの回路定理を使って、ソレノイドがつくる磁場Hを求めてみよう。図のA→B→C→D→Aという閉回路を考えると、AB間のH・dsのみがHlという値を持ち、そのほかの経路ではこの値は0になる。
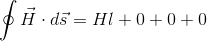
また、1mあたりの巻き数がnのとき、l〔m〕の長さの巻き数はnl回と表されるので、いま考えている閉回路の内部を通過している電流は、nlI〔A〕である。よって、
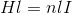
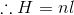
となる。

また、あとのページで紹介するストークスの回路定理
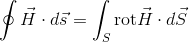
および、電流Iと電流密度iの関係式
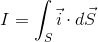
を使えば、
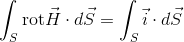
となる。積分範囲が等しいから積分記号が外せて、

という式が導ける。この関係が成り立つことを、アンペールの法則という。
