ナビエ・ストークス方程式
ニュートンの粘性法則

粘性のない非圧縮性流体を完全流体と呼ぶ。今回は粘性のある非圧縮性流体を考えよう。流体の上部に板を置いてx方向に移動させると、板にひきずられて流体が移動する。ただし、底面に接した部分の流体の速度は0である。このように、流速が直線状に変化するような流れを、クェット流れと呼ぶ。ここで、位置yの流体がその上部(y+dy)の流体から引きずられるようにはたらく応力τを考え、これを粘性応力と呼ぶことにする。流速v_xのy方向のずれを考えて、粘性応力がその割合(速度勾配)dv_x/dyに比例するとしよう。

これをニュートンの粘性法則と呼び、比例定数μを粘性率(粘性係数)と呼ぶ。

水平な円管の内部を粘性流体が流れるとき、粘性によってそのエネルギーEが減少するが、流速vは減少しない。ベルヌーイの定理を思い出すと、

運動エネルギーと位置エネルギーが減少しないということから、第3項の圧力pが減少することが分かる。そこで、圧力の減少量Δp(<0)を加えて、

と補正することにする。これを拡張されたベルヌーイの定理と呼ぶ。

流れに沿って圧力が減少することを踏まえて、半径Rの円管を流れる粘性流体の速度分布を求めてみよう。図のような流れをハーゲン・ポアズイユ流れと呼ぶ。

円管の中心部の小さな円柱(断面の半径r、長さL)に注目して力のつり合いの式を立てると、
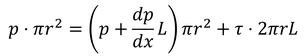
となる。クェット流れとは異なり、r方向の速度勾配が負なので、粘性応力も負である。そこで、
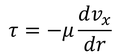
とする。これを力のつり合いの式へ代入してまとめると、

になるので、これを積分することで、

速度分布が得られる。円管の半径がRのとき、r=Rで速度がv_x=0であることを用いて積分定数Cを求めると、

となるので、
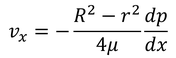
である。これを円管の断面S全体で足し合わせると、
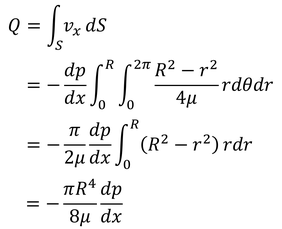
単位時間に断面を通過する流体の体積(流量)が得られる。これをハーゲン・ポアズイユの法則と呼ぶ。
ナビエ・ストークス方程式

x軸に垂直な面にはたらくy方向の粘性応力をτ_xy、y軸に垂直な面にはたらくx方向の粘性応力をτ_yxとする。力のモーメントのつり合いより、これらは等しい。そこで、これらを
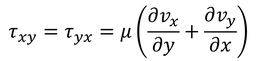
と表そう。すると、τ_xxやτ_yyは、
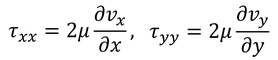
と計算できる。これらを使って、体積ΔxΔyΔzの部分にはたらくx方向の粘性応力による力の和f_xを求めると、

となる。ρΔxΔyΔzで割ると、
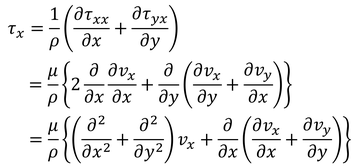
単位質量当たりの粘性応力が得られる。これを3次元に拡張すると、
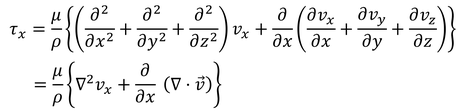
と表すことができる。ここで、非圧縮性流体の場合は∇・v=0だから、

になる。これをオイラーの方程式
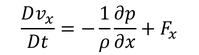
の右辺に加えると、
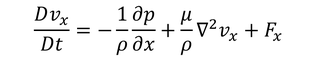
非圧縮性粘性流体に拡張することができる。3成分をまとめて、

と書くこともできる。これを、非圧縮性流体におけるナビエ・ストークス方程式と呼ぶ。左辺を慣性項、右辺第1項を圧力項、第2項を粘性項、第3項を外力項と呼ぶ。ここで、粘性項の係数
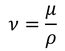
を動粘性率(動粘性係数)と呼び、運動する流体の加速しやすさを表している。これを使ってナビエ・ストークス方程式を書き換えると、
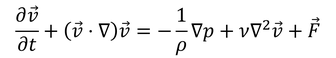
となる。次は、外力F=0のとき、
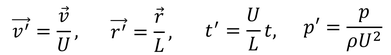
と変換することを考える。Uは流体の代表速度で、Lは代表長さという。物体を通り過ぎる流体の運動では、流れに垂直な幅の長さがL、円管を流れる流体の運動では円管の直径がLである。t'による偏微分は、
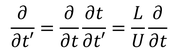
であり、x',y',z'による偏微分をまとめて、
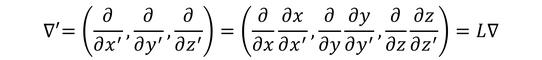
このことから、

と表せるので、ナビエ・ストークス方程式が、
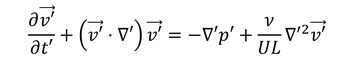
と書き換えられる。粘性項の係数の分母

をレイノルズ数と呼び、粘性項と慣性項の影響の割合を示している。

レイノルズ数が小さいときは粘性項の影響が大きく、流れのそろった層流になる。レイノルズ数が大きいときは慣性項の影響が大きく、個々の流れが卓越する乱流になる。
