ストークスの抵抗法則
ストークス流れ
非圧縮性流体に外力がはたらかないとき、ナビエ・ストークス方程式は、

と表される。レイノルズ数が小さく、移流項(左辺第2項)が無視できるくらい小さいときは、
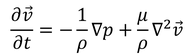
になる。これをストークス流れと呼ぶ。今回はさらに、定常流を扱おう。すると、
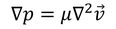
となる。この流れの特徴をつかむために、両辺の発散を取ると、
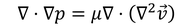
となり、これは

と書き換えることができる。非圧縮性流体では流速vの発散が0
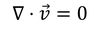
だから、
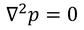
となる。ラプラシアンが0になるような関数を調和関数と呼ぶ。圧力pは調和関数である。他にも、今回考えているナビエ・ストークス方程式の回転を取ると、
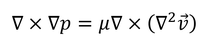
この左辺は0になるので、
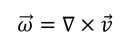
とおくと、
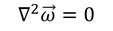
となる。ωを渦度と呼び、渦度は調和関数であることが分かる。
球のまわりの流れ
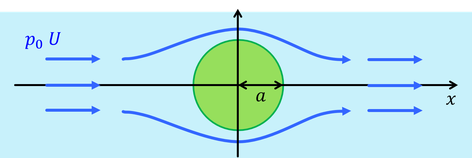
ここからは、球を通過する流体の流れを考えてみよう。圧力pは調和関数であり、無限遠方で一定値になることから、定数項cと、位置rの逆数およびその微分の重ね合わせで表現できる。
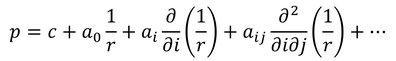
しかしながら、x方向の流れを考えると、定数項以外にx方向に関係のない第2項と第4項以降は省くことができる。そこで、
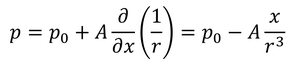
と表そう。無限遠方での圧力をp_0とした。定数Aはあとで求めるので今は置いておく。このラプラシアンを求めたい。

ここで、

であることを利用すると、
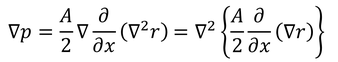
となる。これと、元の方程式
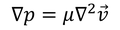
を比較することで、
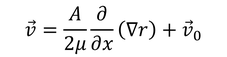
を得る。ラプラシアンの中身の比較なので、不確実性の部分を定数ベクトルv_0で表した。定数ベクトルv_0を決定するために、流速vの発散が0であることを利用して、

微分される量をすべて0とすると、
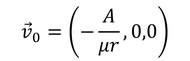
になる。こうして得られたvは、元の方程式の特殊解である。これをv_1と表記すると、各成分は
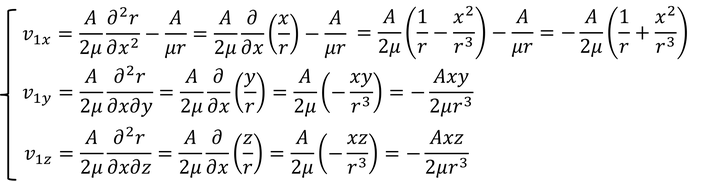
となる。
速度ポテンシャル
元の非斉次微分方程式
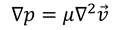
の一般解は、この特殊解v_1と、斉次微分方程式

の一般解v_2の和で表すことができる。v_2は、適当なスカラー関数Φを用いて、
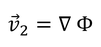
と表される。Φを速度ポテンシャルと呼ぶ。流速v_2の発散が0であることから、
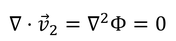
となり、スカラー関数Φが調和関数であることがわかる。調和関数だから、
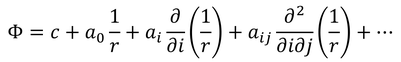
と表せそうであるが、圧力と同様に定数項と、rの逆数のxによる1階微分で表そう。ただし、無限遠方でx方向の流速がUであるためには、
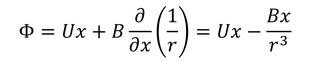
と表される必要があるだろう。
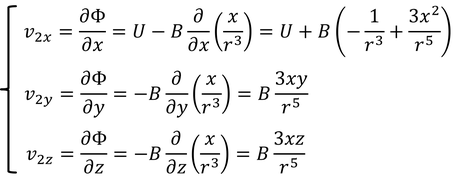
これで、非斉次微分方程式の一般解
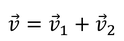
が得られる。成分ごとに表すと、
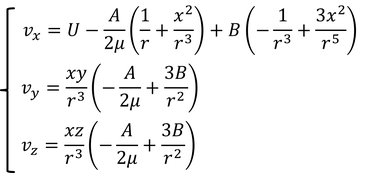
と書ける。では、境界条件によって定数AとBを決定しよう。r=aのときv=0とすると、
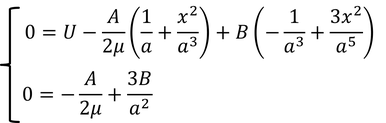
より、
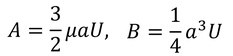
と決まる。これを代入すると、流速vと圧力pが、
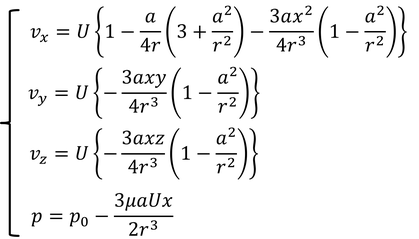
となる。
ストークスの抵抗法則
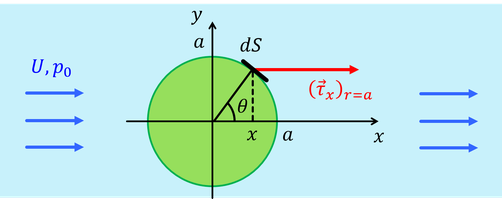
流体中の球体が受ける力を求めてみよう。対称性から、x方向の力だけ考えればよい。半径aの球面上の小さな面積dSの面にはたらくx方向の粘性応力は、

と表すことができる。r=aのまわりで考えていることに注意しよう。ここで、
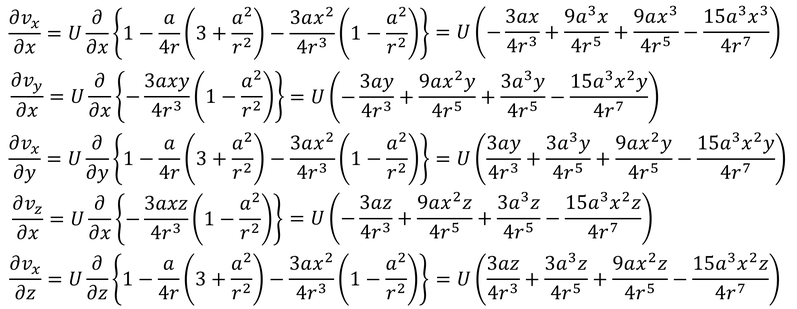
であり、rにaを代入すると、
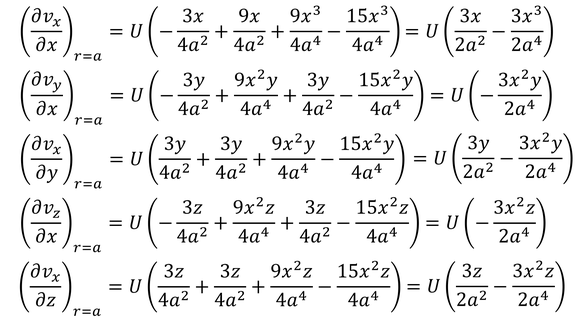
だから、粘性応力による力が、

と計算できる。また、同じように圧力によるx方向の力も、
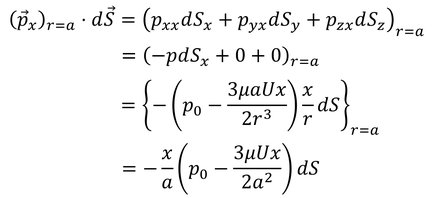
と計算できる。圧力と粘性応力による力の和は、

であり、これは微小な面積にはたらく力だから、球体全体で足し合わせることで、
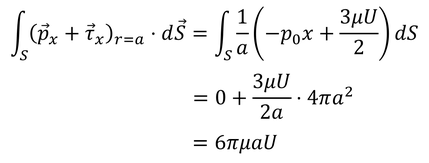
球体全体が流体から受ける力が求められる。これを、ストークスの抵抗法則と呼ぶ。
ミリカンの実験

半径a、密度ρの球が空気中を落下するとき、この球体は重力とストークスの抵抗法則に従う粘性抵抗を受ける。終端速度をv_0とすると、力のつり合いより、
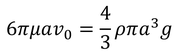
球の半径が、
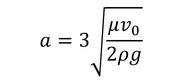
と求められる。また、この球体が正に帯電していて、上向きの電場Eによって上向きに運動しているときを考えよう。終端速度をvとすると、力のつり合いより、

電気量が、
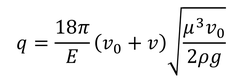
と求められる。ロバート・ミリカンはこうして油滴の電気量を求め、電気素量を求めた。
