力のつり合い

　第１章『力のはたらき』では、力にはいろいろな種類があることを学んだ。今回は物体に複数の力がはたらいているときの力の関係を考えていこう。

　机の上で静止している物体には、重力と机からの垂直抗力がはたらいている。天井から糸でつるされている物体には、重力と糸からの張力がはたらいていて静止している。このように、複数の力が同じ物体にはたらいていてその物体が静止しているとき、それらの力は「つり合っている」という。

　そして、物体に2つの力がはたらいていて力がつり合っているとき、上向きの力と下向きの力の大きさは等しい。これが力のつり合いの関係である。例えば、机の上で静止している物体の重力の大きさが100Nであれば、上向きの力も同じ大きさでなければならないという力のつり合いの関係から、垂直抗力の大きさが100Nであることが分かるのだ。

　もう少し正確に言うと、

一直線上
逆向き
同じ大きさ

の2力は力のつり合いの関係にあるといえる。逆向きでなければならないのはイメージできると思う。一直線上でなければならないのは、少しずれた直線上にある場合、物体が回転してしまうからだ。

力の合成

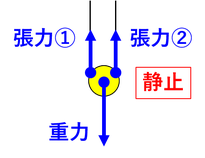
　では、力が3つ以上はたらいている場合の力の関係はどのように表されるのだろうか。例えば上図のような3力の場合、下向きの力が2つに対して、上向きの力が2つはたらいている。このとき、上向きの力の大きさの和が、下向きの力の大きさと等しくなっている。もし、下向きの力がもう1つ加わって4つの力がはたらいている場合にも同じような関係が成り立つ。つまり、

上向きの力の大きさの和と下向きの力の大きさの和が等しい。

このとき、物体にはたらく力はつり合っているといえるわけだ。

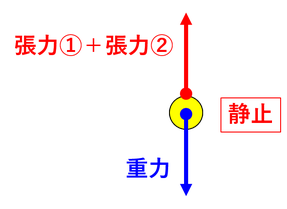
　これは、次のように考えてもいい。張力①と張力②と同じはたらきをする上向きの力を考えて、この1つの力が重力とつり合っていると考えるのだ。すると、先に説明した2つの力のつり合いと見なすことができる。このように、2つの力と同じはたらきをする1つの力を「合力」と呼び、合力を求める操作を「力の合成」と呼ぶ。一般に、同じ向きの2つの力の合力は、

向きは、元の2つの力と同じ向き
大きさは、元の2つの力の大きさの和

になっている。

　次は、こんなことを考えてみよう。張力①とつり合う1つの力があるとすれば、下向きで、張力①と同じ大きさの力のはずだ。この力を、重力と張力②の合力と考える。この合力の大きさは、張力①と同じ大きさであることから、「重力の大きさ－張力②の大きさ」であるともいえる。一般に、逆向きの2つの力の合力は、

向きは、元の2つの力のうち、大きな力と同じ向き
大きさは、元の2つの力の大きさの差

になっている。

　もう一つのパターンを紹介しよう。2つの力が一直線上にない場合の合力は、図のように

元の2つの力を2辺に持つ平行四辺形を書いて、
対角線を結ぶ

ことで求めることができる。これを「平行四辺形の法則」と呼ぶ。

力の分解

　力の合成とは逆に、1つの力と同じはたらきをする2つの力を求める操作を「力の分解」と呼び、分解によって現れた2つの力を「分力」と呼ぶ。分力は、図のように

元の力を対角線に持つ平行四辺形を書いて、
2辺を矢印に変える

ことで求めることができる。