レンズ

凸レンズ

　虫眼鏡のように中央部がふくらんだレンズを「凸レンズ」、逆に中央部がへこんだレンズを「凹レンズ」という。

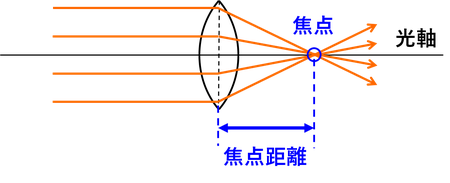
　レンズの中心を通り、レンズに垂直な線を「光軸」という。凸レンズの大切な性質として、光軸に平行な光が光軸上の1点に集まるというものがある。このとき、集まった点を「焦点」といい、レンズの中心から焦点までの距離を「焦点距離」という。焦点はレンズの前後合わせて2か所ある。光がレンズを通る前の方を「レンズの前」、レンズを通った後の方を「レンズの後」と呼ぶことにする。

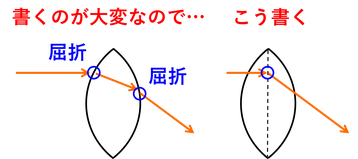
　ところで、レンズを通過する光は、空気とレンズの境界2か所で屈折して進むのだかが、これからレンズを通過する光を書く場合、2回屈折する図を書くのは面倒なので、中心線の位置で折れ曲がったように書くことにする。実際にレンズの途中で屈折しているわけではないので注意して欲しい。（作者はそう思っていた。）

倒立実像

　凸レンズを通過する光の特徴を3つ覚えておこう。

光軸に平行な光は焦点を通過するように屈折して進む。
レンズの中心と通過する光はそのまま直進する。
手前の焦点を通過した光は、レンズを通過後、光軸に平行に進む。

この3種類の光を書いてみると、レンズの後ろで1点に交わる。当然、この3本以外の光も同じ1点に集まっている。ここで、この光の交点の位置にスクリーンを置くと、像が現れる。この像は元の物体と上下・左右が逆向きなので、「倒立像」と呼ばれる。また、実際に光が交わることで現れる像なので、「実像」ともいう。これらを合わせて「倒立実像」とも呼ばれる。

　レンズの一部を隠すと、像を作り出す光の量が少なくなるので、像は少し暗くなる。ただし、全体は映る。

　次は、物体の位置と像の倍率について考えよう。レンズの中心から物体の位置までの距離をa(m)，像の位置までをｂ(m)とすると、相似な三角形の関係から、

という関係が分かる。この関係を使って、物体の位置を変えながら像の倍率を調べていくと、

aが焦点距離の2倍より大きい　→　倍率＜１
aが焦点距離の2倍　→　倍率1倍（物体と同じ大きさ）
aが焦点距離の2倍より小さい　→　倍率＞1

となっていることが分かる。ぜひ図を書いて確かめておこう。

正立虚像

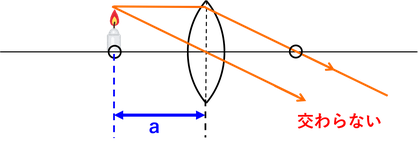
　さらに物体の位置を変えながら実験を続けて、物体の位置を焦点の位置に合わせると、像は消える。これは、レンズを通過した光がすべて平行になり、レンズの後ろで光が交わらないためだ。

　物体の位置を焦点の位置よりもレンズ側に移動させると、レンズを通過した光が互いに広がって進むようになる。当然交わることはなく、どこにスクリーンを置いても実像はできない。

　ところが、このレンズを、レンズの後ろからのぞき込むと、本当の物体よりも大きな像がレンズの前側に現れる。これは、人の目には光が直進して進むように見えるためで、レンズの前方の1点から光が広がっているように見えるからである。このように、実際に光が交わらずに現れる像を、「虚像」といい、物体と同じ向きなので「正立像」という。これらは合わせて「正立虚像」とも呼ばれる。

　正立虚像の倍率も、倒立実像のときと同じく、図を書いてみると分かる。相似な三角形の関係から、

となる。倒立実像のときと同じ式になっている！！

　中学の範囲ではないが、凹レンズも紹介してみよう。光軸に平行な光が凹レンズを通過すると、光は光軸上で、レンズの前方にある1点から広がるように進む。この点を「焦点」といい、レンズの中心から焦点までの距離を「焦点距離」という。焦点はレンズの前後合わせて2つある。

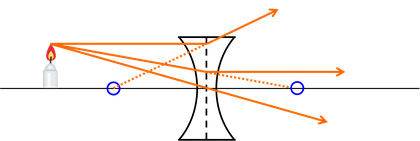
　凹レンズを通過する光の特徴も、3つ頭に入れておこう。

光軸に平行な光は、レンズを通過後、レンズの前方にある焦点から出ているように進む。
レンズの中心を通る光は、そのまま直進する。
レンズの後方の焦点へ向かう光は、レンズを通過後、光軸に平行に進む。

これだけ書いても分かるように、凹レンズは光を結ばない。だから凹レンズによって実像はできない。

　ただし、凹レンズも後方からのぞき込むと、レンズの前方に本物の物体よりも小さな、正立像が見える。これも虚像なので、まとめて「正立虚像」である。

　凹レンズが作る正立虚像の倍率も、これまでと同様に相似な三角形の辺の長さの関係から、

となっていることが分かる。凸レンズと同じだ！