中学物理

電流と電圧 ←→ 電気エネルギー

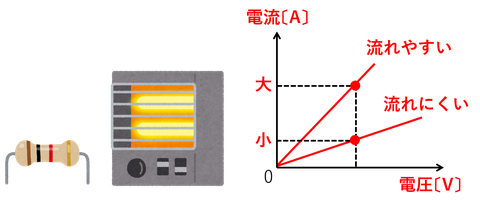
　電熱線などの「抵抗」を電源に接続すると電流が流れる。電源の電圧を調節して、抵抗に加わる電圧を変えながら回路を流れる電流を測定すると、電流と電圧が比例関係にあることが分かる。このきまりを「オームの法則」と呼ぶ。

　電流を縦軸に、電圧を横軸に取ったグラフを見ると、原点を通る直線になっている。このグラフを見ても、電流と電圧に比例関係があることが分かるが、ここでは傾きに注目してみよう。グラフの傾きは、「縦の変化／横の変化」で計算できる。いまは「電流／電圧」だ。すると、傾きが大きいほど同じ電圧のときに大きな電流が流れていることが読み取れるので、傾きが大きいほど電流が流れやすいということが分かる。つまり、

• グラフの傾き（電流／電圧）は、電流の流れやすさ

を表しているということだ。

　すると、電流の流れにくさの計算も簡単に思いつく。「電流／電圧」という計算の分子と分母を入れ替えてやればよいのだ。

• 「電圧／電流」は電流の流れにくさ

　銀や銅、鉄などは電流をよく通すので、抵抗が小さい。このような物質を「導体」という。例えば銅の抵抗値は、1m,1mm2あたり0.016Ωしかない。そのため、導線に用いられる。

　ガラスやゴム、ポリエチレンなどにはほとんど電流が流れない。このような物質を「不導体」という。例えばガラスの抵抗値は10の15乗以上という大きな値である。

　導体と不導体の中間的な抵抗値を持つ物質を「半導体」という。例えばケイ素などがある。

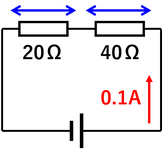
　オームの法則を使って具体的な問題を解いてみよう。20Ωの抵抗と40Ωの抵抗を電源に直列につないだところ、0.1Aの電流が流れた。このとき、電源の電圧は何Vだろうか。

　この問題を解くにはまず、2つの抵抗に加わっている電圧をそれぞれ求める必要がある。ここで必要になるのがオームの法則だ。元の「抵抗＝電圧／電流」の式を、

と書き変える。これで、20Ωの抵抗には20×0.1＝2〔V〕の電圧が、40Ωの抵抗には40×0.1＝4〔V〕の電圧が加わっていることが分かる。ここで、前回の内容で紹介した、電源の電圧は抵抗の電圧の和という関係を使えば、電源の電圧は2+4=6〔V〕であることがわかる。

　電源の電圧が6V，回路を流れる電流が0.1Aであることから、回路全体の抵抗を求めることができる。「抵抗＝電圧／電流」より、6/0.1=60〔Ω〕である。これは、元の抵抗の和（20＋40）になっている。

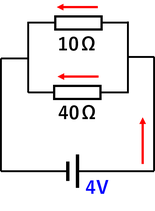
　続いて並列回路の問題も解いてみよう。10Ωの抵抗と40Ωの抵抗を4Vの電源に並列に接続する。電源を流れる電流は何Aだろう。この問題を解くために、まずオームの法則の元の式「抵抗＝電圧／電流」を、

と書き換えたものを用いて、各抵抗を流れる電流を求めておく。抵抗の電圧はどちらも電源の電圧と等しいことも使って、10Ωの抵抗は4/10=0.4〔A〕，40Ωの抵抗は4/40=0.1〔A〕の電流が流れていることが分かる。前回の内容から、電源を流れる電流は各抵抗を流れる電流の和になっているから、0.4+0.1=0.5〔A〕と求められる。

　電源の電圧が4V，電源を流れる電流が0.5Aであることから、回路全体の抵抗が電圧／電流＝4/0.5=8〔Ω〕であることも分かる。この抵抗値は、元の抵抗10Ωや40Ωよりも小さくなっている。

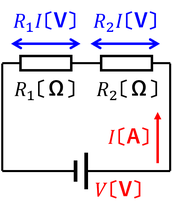
　少し難しいが、直列回路と並列回路の全体抵抗を求める公式を考えてみよう。抵抗値をR1とR2，電源を流れる電流をIとすると、それぞれの抵抗に加わる電圧はR1I，R2Iとなる。すると電源の電圧は

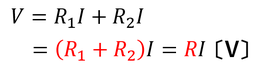
となる。これにより、直列回路の抵抗Rが

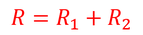
だと分かる。これで、具体的な数値で考えたように、2つの抵抗値の和になっていることが示された。

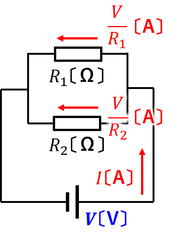
　続いて並列回路について。電源の電圧をVとすると、各抵抗を流れる電流は、V/R1，V/R2となる。すると、電源を流れる電流は

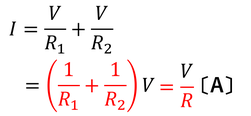
となる。このことから、全体抵抗Rと、R1,R2との関係

を導くことができる。試しにR1=10〔Ω〕，R2=40〔Ω〕を代入すれば

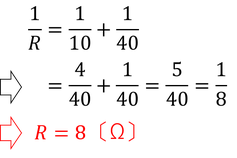
こうして、先に求めていた全体抵抗8Ωを求めることができる。

　直列回路の全体抵抗が元の抵抗よりも大きくなるのは、抵抗が長くなって電流が通りにくくなるからとイメージしよう。並列回路の全体抵抗が元の抵抗よりも小さくなるのは、通り道が増えて、電流が通りやすくなるからだとイメージできる。