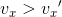力と運動

運動量と力積 ←→ ベクトル

　前回の「運動量と力積」で、2種類の関係式を紹介した。1つ目は上皿天秤型

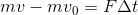
であり、2つ目は時系列型

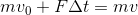
である。これからも自力で関係式を作らなくてはならない場面は多くあるが、その意味を考えながら正しい関係式を作っていこう。

• 運動量の分野では、向きで間違えることが非常に多い。そこで、文字式の中に「ー」記号が含まれていない時系列型の方が、間違える可能性は低いと思われる。

　今回は物体同士の衝突を考えていく。例として、はじめはそれぞれmAvA, mBvBの運動量を持っていた物体A, Bが衝突し、その後、mAvA', mBvB'の運動量に変化したという状況を考えよう。

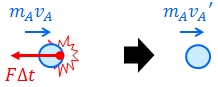
まず物体Aだけに注目する。このとき運動量と力積の関係を表す式は、力積の大きさをFΔt、運動の向きを正の向きとすると、

と書くことができる。

次に物体Bだけに注目すると、運動量と力積の関係は、力積の大きさをFΔt、運動の向きを正の向きとして、

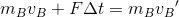
と書くことができる。AとBが衝突したときに互いに及ぼし合う力Fは、作用反作用の関係になっているから、同じ大きさである。

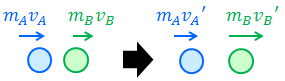
　さて、以上の2式を足し算してみよう。すると、

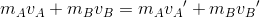
のように、力積FΔtを消去することができる。この式は、「物体AとBの運動量の和が衝突の前後で変化していない」ということを示している。変化していないことを”保存されている”といい、これを運動量保存則という。

　運動量保存則は衝突以外にも、合体や分裂に使うことができる。問題文中のキーワードを見落とさないようにしよう。

• 合体

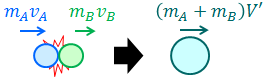
• 分裂

　ボールを床に落としたとき、その跳ね方はボールの種類や床の材質などによって違う。このとき、床と衝突する直前のボールの速さ|v|と直後の速さ|v'|の比

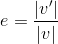
これを反発係数という。衝突の前後で必ず速度の向きが変化することを考えると、この値は速度v, v'を使って、

と表すこともできる。衝突後の速さは衝突前の速さよりも必ず遅くなっていることから、反発係数の値は0～1の範囲に収まることになる。このことをきちんと理解して、分母と分子を逆に計算してしまわないように気を付けよう。「前分の後」が正しい計算だ。

　e=1のときを弾性衝突、それ以外の時を非弾性衝突という。特に、e=0のときを完全非弾性衝突ともいう。完全非弾性衝突は、べちゃっと床にくっついてしまったときだ。

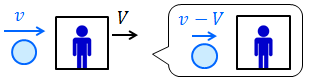
　では、衝突相手が動いているときの反発係数はどう考えたらいいのだろうか。例えば、速度vのボールが速度Vで動く壁と衝突した場合などが考えられる。しかし、これはボールがv-Vの速度で動かない壁と衝突したときと同様であるとみなせるので、相対速度の比を考えればよいということが分かる。つまり、

速度v,Vの物体同士が衝突し、それぞれ速度がv', V'に変化したとすると、そのときの反発係数eは

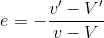
と表すことができるということである。この公式を使う上で気を付けて欲しいことは次の3点。

1. 衝突前が分母で、衝突後が分子であること。「前分の後」！
2. どちらに対する相対速度なのかが、分母と分子で一致していること。つまり(v-V)と(V-v)がごちゃまぜにならないこと。
3. 分数の前の「ー」を忘れないこと。

問題

　0.05kgの物体Aと0.1kgの物体Bがそれぞれ3m/s, 2m/sで正面衝突した。衝突後のA, Bの速度をそれぞれ求めよ。ただし、A, B間の反発係数を0.8とする。

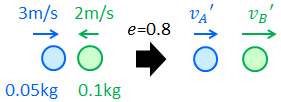
→衝突前のAの運動の向きを正とする。衝突の問題だから、運動量保存則より、

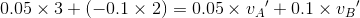
また、反発係数が0.8であることから、反発係数の式より、

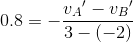
以上より、

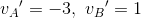
よって、衝突後のAの速度は衝突前とは逆向きに3m/s、衝突後のBの速度も衝突前とは逆向きに1m/sであることが分かった。

　これまでは一直線上の運動ばかりを扱ってきたが、運動量と力積の関係や運動量保存則は、平面内でも成立する。ただし、このときには速度のx成分, y成分ごとに成り立っているということに注意。

　続いて平面内の運動における反発係数の式も説明しておく。この場合には、衝突面に垂直な方向の速さの比が反発係数になるので、

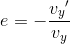
である。また、摩擦のないなめらかな面との衝突の場合には、衝突面方向の速度は変化しない。

• 摩擦力がはたらかない場合

• 摩擦力がはたらく場合