ベクトル
速さや温度のように、大きさしか持たない量のことをスカラーという。これに対して、速度や加速度、力のように、大きさと向きを併せ持つ量のことをベクトルという。
ベクトルの表し方
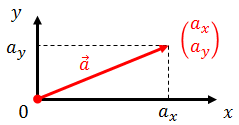
ベクトルaの表し方には2種類ある。1つ目は矢印で図示するという方法。これで向きと大きさを表すことができる。もう1つは、矢印の始点を原点(0,0)として、終点の座標(ax,ay)で表現するという方法だ。これをベクトルの成分表示という。
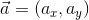
このとき、ベクトルの大きさ|a|は三平方の定理から、
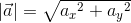
と計算できる。
ベクトルの和と差
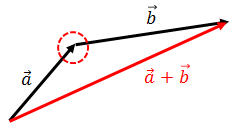
速度の合成のときに学んだように、ベクトルの和は2種類のベクトルをつなげて描き、1つ目のベクトルの始点から2つ目のベクトルの終点に向かう矢印を描けばいい。
成分表示でも説明できる。いま、2つのベクトル

があったとき、その和は
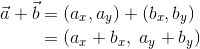
と計算できる。蛇足だが、ベクトルの和や差を成分で計算する場合には成分を縦に並べて、
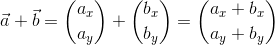
と書いた方が見やすい。縦に並べるか横に並べるかは、今のところどっちでもいいので見やすい方を使おう。
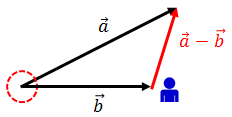
ベクトルの差は、相対速度を学んだ時のように2つのベクトルの始点を揃えて描き、自分から相手に向かって新しい矢印を描けばいい。a-bの場合、aが相手でbが自分だ。
ベクトルの差も、ベクトルの和と同じように成分ごとに計算することができる。
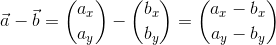
単位ベクトル
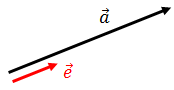
あるベクトルa=(ax.ay)と、向きが同じで大きさが1のベクトルeを、ベクトルaの単位ベクトルという。
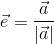
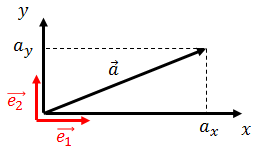
また、x軸、y軸方向の単位ベクトルを基本ベクトルという。x軸方向の基本ベクトルをe1, y軸方向の基本ベクトルをe2と書くことにすると、ベクトルaはこれらの基本ベクトルを使って、
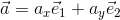
と表すことができる。これをベクトルaの基本ベクトル表示という。いまの計算をベクトルの成分で表現すると、
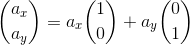
である。
ベクトルの内積
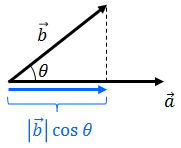
2種類のベクトルについて、同じ成分どうしを掛け算した結果のことをベクトルの内積という。ベクトルaとベクトルbの内積は次のように「・」で表現する。
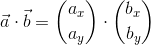
また、上図のように2種類のベクトルa,bの間の角度θが分かっているとき、その内積は、ベクトルaの長さが|a|、ベクトルbのベクトルa方向の成分が|b|cosθだから、
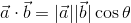
と計算することができる。θ=90°のときはcos90°=0だから、この計算結果は0になる。つまり、2種類のベクトルが直交している場合、その内積は0になるということ(下図)。内積の最重要な性質なので、必ず覚えておこう。
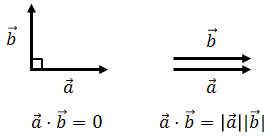
次は成分の計算で内積を考えたい。そこでベクトルaとベクトルbを基本ベクトルを用いて次のように表して、
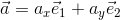
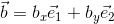
この積を計算しよう。

ここで、基本ベクトルは大きさが1であり、またe1とe2は直交しているから
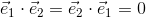
であり、これを用いれば、
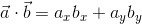
と求めることができる。
ところで、これまではxy平面上のベクトルばかりを扱ってきたが、xyz空間上のベクトル
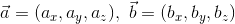
を扱うことにすれば、その内積は、
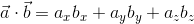
になる。
ベクトルの外積
2種類のベクトルについて、直交する成分どうしの掛け算の結果をベクトルの外積という。外積は「×」で表す。
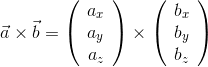
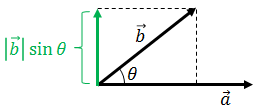
また、上図のように2種類のベクトルa,bの間の角度θが分かっているとき、その外積の大きさは、ベクトルaの長さが|a|、ベクトルbのベクトルaと直交した方向の成分が|b|sinθだから、
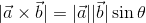
と計算することができる。θ=0°のときにはsinθ=0だから、外積は0になる。つまり、2種類のベクトルが平行なとき、その外積は0になるということ(下図)。
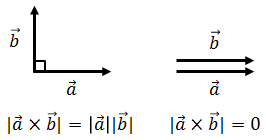
さて、内積には向きがなかったので大きさが計算できればそれでよかったが、外積には向きがあり、下図のように外積a×bの向きはa→ bと回転した右ねじが進む向きと決められている。
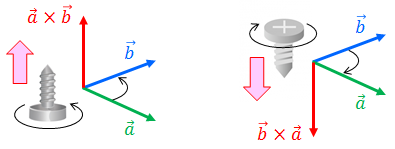
だから、外積a×bと外積b×aのあいだには
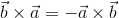
という関係が成り立っていることになる。また、x, y, z軸方向の基本ベクトルe1, e2, e3のあいだには、
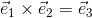
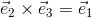
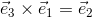
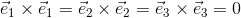
という関係が成り立っている。
それでは最後に、ベクトルの成分で外積を表そう。3次元ベクトルaとbを基本ベクトルを使って次のように表して、
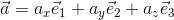
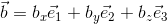
基本ベクトルの外積に注意して、この積を計算すれば、
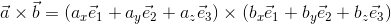
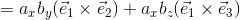
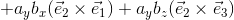
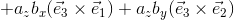
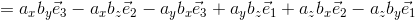
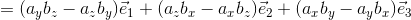
よって、
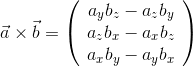
と表せる。
