運動量と力積
ニュートンは著書『プリンキピア』の中で、「力とは、”運動”の時間変化率に相当するものである」と述べている。運動を大きく変化させるためには大きな力が必要だろうし、運動を短期間で変化させるためにも大きな力が必要だろうというわけだ。
ところで、このニュートンのいう力を数や式で表すためには”運動”というものを数や式で表す必要がある。では”運動”とはなんだろうか。今回は、この”運動”の量に注目してみよう。
運動量
運動している物体には勢いや迫力がある。そしてそれは、運動している物体の質量や速さが大きいほど大きいように感じる。というわけで、運動の勢いや迫力を表す量として
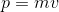
という量を導入してみよう。これを運動量といい、m[kg]は質量、v[m/s]は速度を表している。運動量の単位は[kg・m/s]と書き、キログラム・メートル毎秒と読む。
運動量の定義に使われているv[m/s]は速さではなく速度であることに注意しよう。速度は向きを持つので、運動量も向きを持つ。

問題
144km/hの速さで運動している140gのボールの運動量の大きさp[kg・m/s]を求めよ。
→144km/h=40m/s, 140g=0.14kgだから、公式より
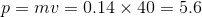
答えは5.6kg・m/s
力積
実は、ニュートンは加速度という形ではなく、冒頭でも述べたように力を「運動量の変化」という形で定義している。式で表すと、時間Δtのあいだに運動量がΔpだけ変化したときの力Fを、
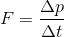
になる。ここで、この式を
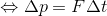
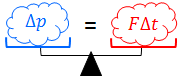
と書き変えたとき、右辺のFΔtを力積(りきせき)という。そこでこの式を「運動量と力積の関係」と呼ぶことにしよう。力積の単位には[N・s]を使い、ニュートン秒と読む。だからこの式は「運動量の変化Δpは力積FΔtに等しい」という意味になっている。バランスの取れた上皿天秤をイメージしてみよう。
ここで、運動量の変化Δpを

と書くと、運動量と力積の関係を表す式は、
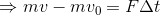
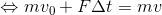
と書き変えることができる。
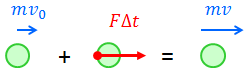
この式は、「はじめ、mv0の運動量を持っていた物体が、FΔtの力積を受け取って、mvの運動量になった」という意味。時間の流れに沿って状況を整理しながら式を作ることができるので、問題を解く場合には上皿天秤型よりもこっちの式の方がおすすめだ。
問題
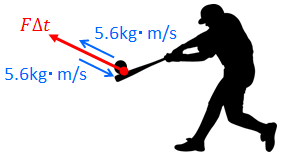
はじめ、5.6kg・m/sの運動量を持っていたボールが打ち返されて、逆向きで5.6kg・m/sの運動量に変わった。このときバットから受け取った力積FΔtを求めよ。
→打ち返される前後で運動量の向きが違うことに気を付けよう。打ち返される前のボールの運動量の向きを正の向きとして運動量と力積の関係式を作ると、
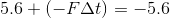
になる。力積の向きも打ち返されたあとのボールの運動量の向きも負の向きだから、マイナスが付いている。あとはこれを解けば、
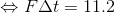
答えは11.2N・s
- この分野では運動量や力積の向きを考慮に入れずに式を作って間違える場合が多いので、正の向きをきちんと定め、正負の向きを確認しながら式を作る癖を付けよう。
平均の力
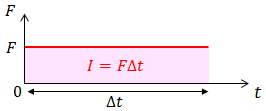
力積Iの定義が
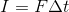
であることを踏まえてF-tグラフを描くと、その面積が力積Iを表していることが分かる。また、運動量と力積の関係
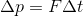
からF-tグラフの面積Iが運動量の変化Δpに等しいことも分かる。
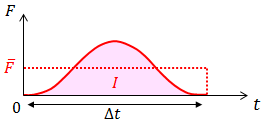
しかし、運動量が変化している間、物体にはたらいている力Fは一定とは限らない。このような場合、はたらいている力を刻一刻と追いかけていくことは難しいが、最終的な運動量の変化Δpと時間Δtを使うことで、平均の力を求めることはできる。
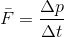
問題
ボールとバットの接触時間が0.02秒間であり、この間にボールの運動量が11.2kg・m/sだけ変化した。このとき、ボールがバットから受けた平均の力を求めよ。
→公式より、
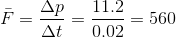
答えは560N
