角運動量
剛体が回転せずに静止しているとき、力のモーメントがつり合っていたのだった。今回は、これまでに学んだ力や運動量の復習をしながら、剛体の回転運動について考えてみよう。
力のモーメントの外積表示
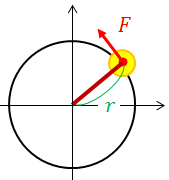
まずは力のモーメントの復習から始める。支点から力の作用点までの距離をr, 力の大きさをFとしたとき、この力が物体を回転させる能力Nを力のモーメントと呼び、
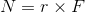
と表した。
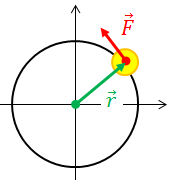
この内容を少しだけ発展させよう。支点(回転の中心)から力の作用点へと向かう位置ベクトルrを考えて、力のモーメントNを次のように表すことにするのだ。
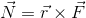
「×」はベクトルの外積。
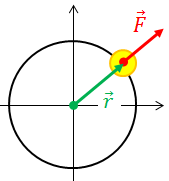
ベクトルAとベクトルBの外積を考えた場合、AとBが平行であるとき外積の値は0になるというのが外積の大切な性質だった。例えば、ベクトルrとベクトルFが平行のとき、この力は物体を回転させる能力を持っていないので、確かに力のモーメントNは0になっている。
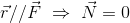
角運動量
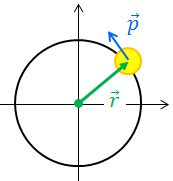
回転運動は力のモーメントがあることで発生するので、これを回転運動の要因と考えることにする。それでは並進運動の要因は何かと言うと、これは力
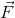
である。
また、並進運動の勢い・激しさを表す物理量が運動量
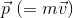
であったから、これを踏まえて、回転運動の勢い・激しさを
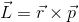
と定義することにしよう。これを角運動量という。
|
|
並進運動 |
回転運動 |
|
運動の要因 |
力
F |
力のモーメント
N=r×F |
|
運動の激しさ |
運動量
p |
角運動量
L=r×p |
角運動量保存則
運動量pを時間tで微分すると、
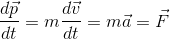
力Fになることが知られているので、これと同じように角運動量Lも時間tで微分してみよう。
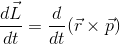
積の微分公式を使って、
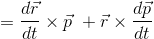
位置rの時間微分が速度v, 運動量pの時間微分が力Fだから、
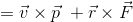
ここで、v//pだからその外積は0となり、またr×F=Nだから、
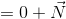
よって、
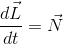
という関係が成り立っていることが分かった。
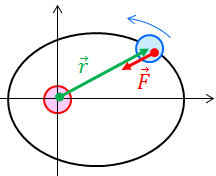
ここで、惑星の運動のように常に同じ1点に向かって力がはたらいている運動を考えてみると、rとFが平行だからN=0であり、
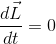
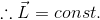
という式が成り立っている。これは、N=0のとき、角運動量Lは時間変化しないということで、これを角運動量保存則という。

ところで角運動量保存則の式を書き変えてみると、
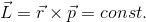
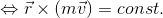
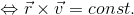
となることから、以前に登場した式を作ることができる。
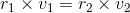
これはケプラーの第2法則(面積速度一定の法則)だ。つまり、この法則は角運動量保存則を言い換えただけだったというわけ。
慣性モーメント
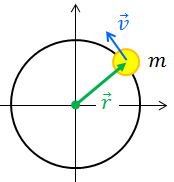
さて、ここからは円運動を考えよう。円運動ではベクトルrとベクトルpが直交しているので、角運動量の大きさLは
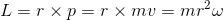
と計算することができる。ただし、
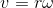
という速度と角速度の関係を使った。また、ここで、
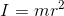
とおけば、元の式は
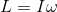
になる。この式と、並進運動の運動量の式
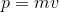
を比較してみると、角運動量Lと運動量p、角速度ωと速度vがそれぞれ対応している。ということは、Iとmもこれらと同じような関係になっているのではないだろうか。そういえば質量mとは並進運動のしにくさを表す量だったから、Iは回転運動のしにくさを表す量だと考えてよさそうだ。これを慣性モーメントという。
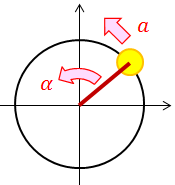
続いて、慣性モーメントIを使って表した角運動量Lの式の両辺を時間微分してみると、
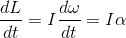
となる。αは角速度ωの時間微分
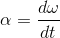
で、角加速度という。また、角運動量Lの時間微分が
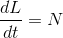
のように力のモーメントNだったことを思い出せば、
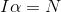
という式を導くことができる。この式は、並進運動の運動方程式
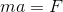
と似ていることから、回転運動の運動方程式とみなすことができそうだ。お疲れ様でした。最後に並進運動と回転運動に関係する物理量を表にまとめてみたので比べてみよう。
|
|
並進運動 |
回転運動 |
|
位置 |
位置x,r |
角度θ |
|
速度 |
速度v |
角速度ω |
|
加速度 |
加速度a |
角加速度α |
|
力 |
力F |
力のモーメントN |
|
動かしにくさ |
質量m |
慣性モーメントI |
|
運動量 |
運動量
p=mv |
角運動量
L=Iω |
|
運動方程式 |
ma=F |
Iα=N |
問題
角度θの斜面上に質量M, 半径Rの球を静かに置いたところ、球は斜面上をすべることなく転がった。このとき、球の斜面方向の加速度aを求めよ。ただし、球の慣性モーメントをIとする。
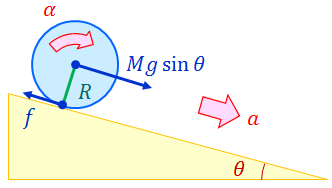
解答
摩擦力をfとすると、斜面方向の運動方程式は、
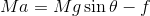
であり、回転運動の運動方程式は、
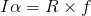
である。また、加速度aと角加速度αの関係は、
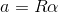
である。
これらの式からαとfを消去する。
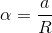
より
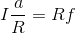
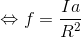
だから、
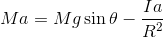
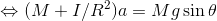
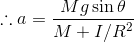
となる。
