力のモーメント
ここまでの内容では、物体の形状や体積を考えることはほとんどしてこなかった。このような物体を質点という。これに対し、大きさを持ち、変形することのない理想的な物体のことを剛体という。今回は、この剛体が静止していられる条件を見ていこう。
力のモーメント
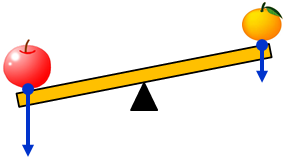
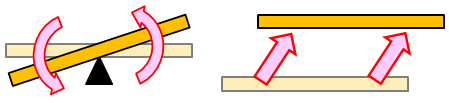
図のようなシーソーを考えよう。重さの異なる物体を両端に乗せると、重たい方へとシーソーは回転する。これは、重たい物体の方が、シーソーを押す力が大きいためだ。

続いて、同じ重さの物体を図のように乗せると、シーソーは支点からの距離が長い方へ回転する。このことから、シーソーが回転する要因には、力Fだけでなく、支点からの距離rも関係していることが分かる。
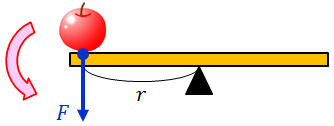
そこで、シーソーが回転する能力の大きさを表す物理量として、次のような量を考えてやろう。
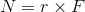
この式は、支点からの距離rが長いほど、またその場所に加わる力Fが大きいほど物理量Nが大きくなることを示している。この物理量Nを力のモーメントという。単位は〔N・m〕。
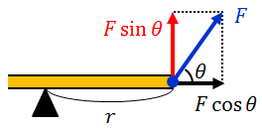
ここで1つ注意。力Fが図のように斜め方向にはたらいている場合、シーソーを回転させるのはシーソーに対して垂直な成分F sinθだけで、シーソーに平行な成分F
cosθは回転運動には影響を与えない。だから、この状況における力のモーメントNは
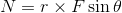
ということになる。
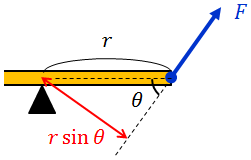
また、同じ結果を導くためには、力Fの作用線を伸ばして、その作用線と支点の距離r sinθを考えてもいい。
状況に応じて使い分けよう。
力のモーメントのつり合い
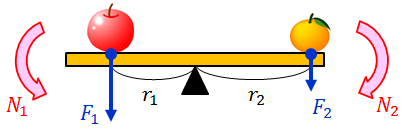
次はシーソーが回転しない条件を考えてみよう。上図の状況のとき、力F1はシーソーを左回りに回転させようとしていて、力F2はシーソーを右回りに回転させようとしている。それぞれの力のモーメントは、
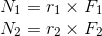
と表されるわけだが、力のモーメントとはシーソーを回転させる能力のことだったから、左回りの力のモーメントN1と右回りの力のモーメントN2が等しければ、全体として回転する能力がないということになるのでシーソーは回転しない。
これを力のモーメントのつり合いという。
物体が平行に移動していく運動のことを並進運動という。質点が並進運動せずに静止していられるための条件は力のつり合いだけだったから、
- x軸方向の力のつり合いの式
- y軸方向の力のつり合いの式
を立てればよかった。しかし剛体の場合、並進運動だけでなく回転運動しないことも静止条件に必要なので、これらの式に加えて
- 力のモーメントのつり合いの式
を立てる必要があるのだ。
問題
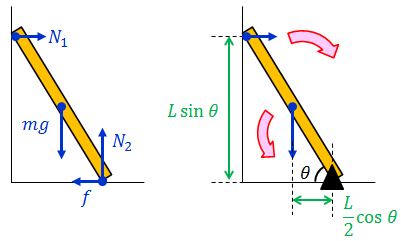
滑らかな壁に立てかけられて静止した長さL, 質量mの棒状の剛体にはたらく垂直抗力および摩擦力の大きさN1,N2,fをすべて求めよ。ただし、床と棒のあいだの角度をθ, 重力加速度をgとする。
解答
まず、この剛体が並進運動しないためには力がつり合っている必要があるから、水平方向の力のつり合いより
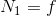
鉛直方向の力のつり合いより
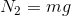
また、この剛体が回転運動しない条件も必要だから、床との接点のまわりの力のモーメントのつり合いより、
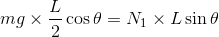
これらを解いて、
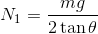
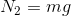
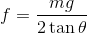
補足
解答では回転の中心を床との接点としたが、他点を回転の中心として考えても構わない。例えば、壁との接点を回転の中心として、このまわりの力のモーメントのつり合い
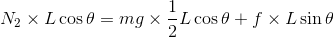
を考えてもいいし、重力の作用点(重心)のまわりの力のモーメントのつり合い
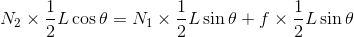
を考えてもいい。
重心
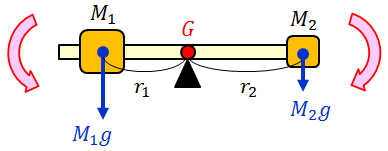
図のように質量分布に偏りのある剛体でも、どこか1点で支えることができる。この点を重心と呼ぶ。重心の位置Gは、力のモーメントのつり合いより、
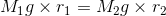
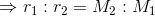
という条件を満たす点であることが分かる。回転中心からの距離の比が、質量の逆比に等しいということだ。
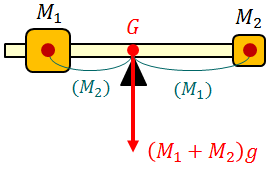
また、重心は剛体の質量がすべてその一点に集中したと仮定したときの重力の作用点と考えることもできる。
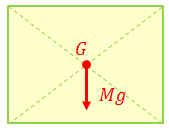
剛体の形状によっては重心の位置が分かりやすい。
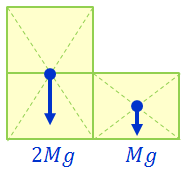
それでは、質量Mの長方形を図のように3枚並べたときの重心の位置を求めてみよう。左側2枚の重心の位置と、右側の1枚の重心の位置はすぐに分かるので、
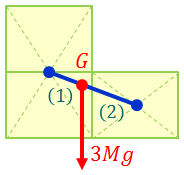
これらの点を1:2に内分した点が、全体の重心ということになる。
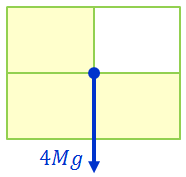
ところで、今の問題は次のように考えることもできる。切り取られた部分を質量Mの板で埋めたときにできる、質量4Mの大きな長方形の重心は、明らかにその中心で、
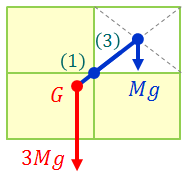
この点は、3枚の長方形の重心Gと、切り取られた長方形の重心を1:3に内分する点になっているはずである。このように、切り取られた部分を利用して重心を求めることもできる。
