指数・対数
物理では宇宙の世界から原子の世界までを扱うので、非常に大きな数も非常に小さな数も登場する。例えば、
- 真空中での光の速さ 300000000m/s
- 水素原子の大きさ 0.0000000001m
など。大変だけど0を数えてみると、それぞれ8個と10個ある。ぱっと見わかりにくいので、この数字を
3×108m/s, 1×10-10m
と表そう。これを指数表示という。
指数
数値を10のn乗と表すとき、その数値が10倍になると、右肩の数(指数)は1ずつ増える。
101=10, 102=100, 103=1000, 104=10000
同じように考えると、数値が1/10になると指数は1ずつ減ることになるから、
100=1, 10-1=0.1, 10-2=0.01, 10-3=0.001, 10-4=0.0001
ということになる。
指数を使った数値の計算は、慣れないうちは0を並べる書き方に直してからもう一度直すほうが安心するかもしれないが、限界があるので指数のままできるように練習しよう。基本は
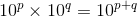
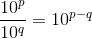
の2つ。掛け算が指数の足し算になり、割り算が指数の引き算になっていることに注目だ。このことが分かれば、
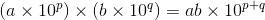
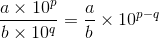
のように、10n部分とそのほかの部分とを別々に計算する方法が次第に分かってくる。あとは慣れが重要なので、たくさん練習を積んで、早く安心できるようになろう。
対数
10をp乗した結果をPと書くことにすると、
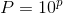
という関係式ができるが、同じ内容でもこの式を「p=」と表したいときもある。つまり、10を何乗したらPになるのか知りたい! という場合だ。そこでこれを
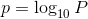
と表そう。このとき、「pは10を底(てい)とするPの対数」という。今のように、自然科学では10を底に持つ対数を使うことが多く、これを常用対数という。
さて、対数の性質を考えていくが、とりあえず
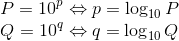
という2種類の数を考えよう。P×Qを計算すると、
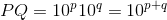
となるので、この式を対数表示に直せば、
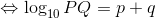
と書くことができる。ここでさらに、pとqをそれぞれ対数表示に直せば、
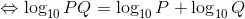
という関係を導くことができる。PとQの掛け算を、対数どうしの足し算に変えることができるのだ。
同じようにP/Qの計算をすると、
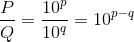
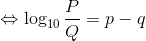
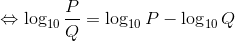
という関係を導くことができる。今度はPとQの割り算を、対数どうしの引き算に変えることができるのだ。
- 対数の発明が天文学を飛躍的に向上させたと言われている。天文学では大きな数値を扱うことが多く、掛け算や割り算には限界があるためだ。
さて次は、
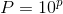
の両辺をr乗しよう。
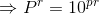
ここで、この式を対数で表現し直して、
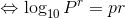
さらにpを対数に直すと、
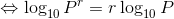
という関係を導くことができる。Pの指数rをlogの前に出すことができるということで、ずいぶん計算が楽になる。
対数の重要な公式をまとめておこう。
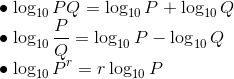
ネイピア数
自然科学で多く用いる対数には、常用対数のほかに自然対数と呼ばれるものがある。自然対数とはネイピア数eを底に持つ対数のことで、
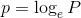
のように表される。上で導いた対数の3公式は、常用対数だけでなく自然対数でも使用できるということも知っておこう。
ところでネイピア数とは、
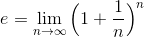
と定義される値である。この式の( )の内部は0に近づいていくが、指数nが∞に発散していくため、値がはっきりしない。そこで、nに具体的な数値を代入して計算してみる。
| n | e | n |
e |
| 1 |
2.00000 |
10 |
2.59374 |
| 2 |
2.25000 |
100 |
2.71692 |
| 3 |
2.37037 |
1000 |
2.71815 |
| 4 |
2.44141 |
10000 |
2.71827 |
| 5 |
2.48832 |
∞ |
2.71828 |
すると上の表のような結果になり、ネイピア数eは約2.71828に収束していくことが分かる。この中途半端な数値を考えることで何かいいことがあるのか? と問われそうだが、答えは「大あり」だ。
例えば、exを微分してみたときにその強力な効果が表れる。計算してみよう。微分の定義より
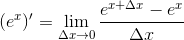
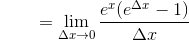
ここで、
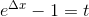
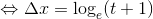
とおくと、
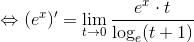
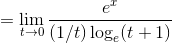
さらにここで 1/t=n とおけば、
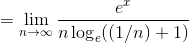
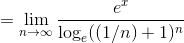
だから、あとはネイピア数の定義を使って、
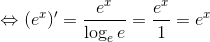
と求めることができる。なんと、微分してもその姿が変化しない! その理由でこの関数は非常によく使用される。
さて、今度は自然対数logexの微分を計算してみよう。微分の定義より、
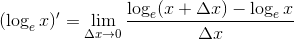
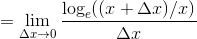
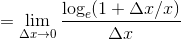
ここで x/Δx=n とおくと、
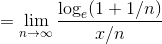
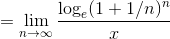
よって、
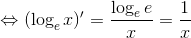
意外と簡単な形になったでしょ? この関係を使って、次の問題に挑戦しよう。
空気抵抗を受ける落下運動
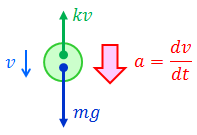
最後に、空気抵抗を受けるボールの落下運動について考察してみよう。速度がvのとき、ボールは進行方向とは逆向きにvに比例する空気抵抗kvを受けるとする。加速度の大きさをa=dv/dtとして運動方程式を立てて解く。
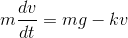
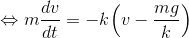
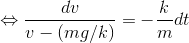
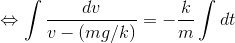
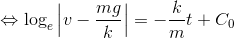
C0は積分定数。また、絶対値| |の中は常に正だから、
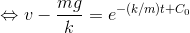
と変形できる。さらに、eC0=C(定数)とすると、
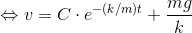
それでは、初期条件を与えて具体的にCを定めよう。時刻t=0のときの速度をv=0とすると、
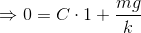
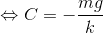
となるので、t秒後の速度vを表す式が導ける。
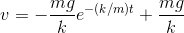
この関係をv-tグラフに表すと下図のようになる。t→∞のときの速度 vf=mg/k を終端速度という。