万有引力の導出
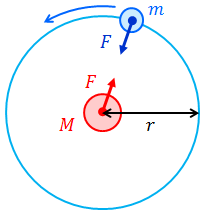
万有引力の公式を導出してみよう。惑星の運動を等速円運動だと考えると、円運動の運動方程式
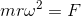
は、角速度 ω=2π/T が一定だから、

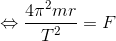
になる。ここで、ケプラーの第3法則を等速円運動に適用すれば「T2/r3=k(一定)」という式が成り立つことになるから、
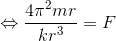
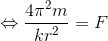
という式ができる。この式は、太陽から距離rだけ離れた位置にある質量mの惑星が、太陽から受けている力Fmを表している。
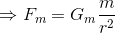
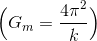
ところで、作用反作用の関係から、逆向きで同じ大きさの力FMが太陽にはたらいているはずである。Fmとの対称性から、この力は太陽の質量Mに比例し、rの2乗に反比例すると考えられる。
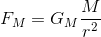
FmおよびFMの関係を同時に満たす式は、
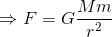
である。これで万有引力の式が導出できた。
ところが、実際の惑星の軌道は太陽を1つの焦点とする楕円である。そこで、これからは楕円軌道上を運動する惑星の動きを考えて万有引力の式を導出してみよう。
楕円の方程式
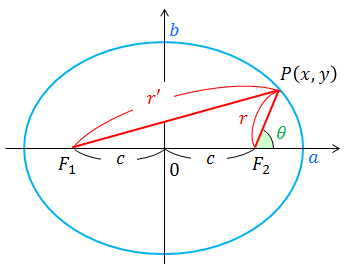
まずは楕円の方程式を求める。楕円とは、2点(F1,F2)からの距離の和(r'+r)が常に一定な図形のことである。つまり、
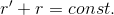
という関係がいつも成り立っているわけだ。const.は定数の意味。
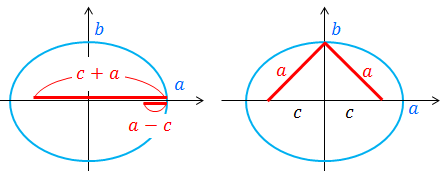
ここで、楕円上の点P(x,y)を(a,0)に移動させると、
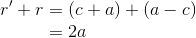
であると分かり、また、点P(x,y)を(0,b)に移動させると、r'=r=aだから三平方の定理より、
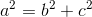
という関係も分かる。
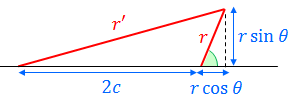
ここで、x軸と直線F2Pの間の角度θ使って r' を表すと、三平方の定理から
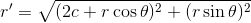
になる。この式を「r'+r=2a」を用いて変形していくと、
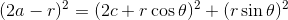
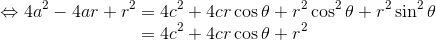
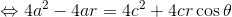
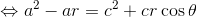
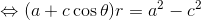
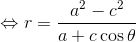
ここで「a2-c2=b2」の関係を使えば、
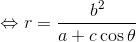
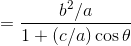
となるから、いま、
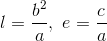
とおくと、
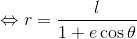
になる。これを楕円の方程式と呼ぶことにしよう。
次の話へ進む前に、rと同じようにaとbをl,eで表しておく。lとeの定義式から
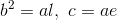
これを「a2=c2+b2」に代入して変形すれば、
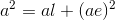
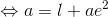
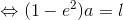
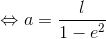
が求まる。さらに、この結果を「b2=al」へ代入すると、
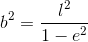
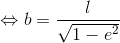
が求まる。あとで使うことになるので、必要になったらまたここへ戻ってこよう。
ケプラーの法則
さて、これまでは一般的な楕円の話であったが、いま考えているのは惑星の運動だから、次はケプラーの法則を詳しく見ていく。
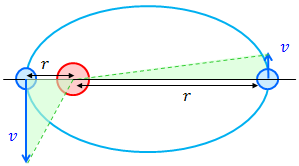
ケプラーの第2法則は「惑星が一定時間内に掃く面積は一定である」という内容だった。これは面積速度一定の法則とも呼ばれ、面積速度Vは
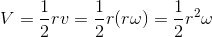
と表せるから、定数hを使って、面積速度一定の法則を
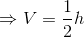
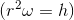
と表現しよう。
ケプラーの第3法則は「惑星軌道の長半径aの3乗は周期Tの2乗に比例する」という内容だったから、定数kを使って、
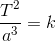
と表現しよう。
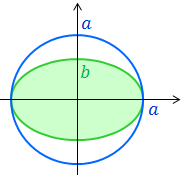
ところで、楕円の面積Sは
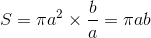
であり、周期Tのあいだにこれだけの面積を惑星が”掃く”わけだから、面積速度Vは

と書くことができる。ここで、ケプラーの第2法則「V=h/2」を使ってこの式をTについて解けば、
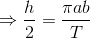
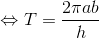
になるから、ケプラーの第3法則の式を、
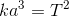
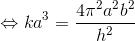
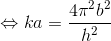
と変形し、さらにa,bをl,eで表せば、
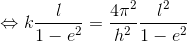
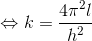
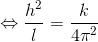
と変形することができる。左辺のlやhは1つの惑星の運動に対する変数だが、右辺のkは太陽系の惑星すべてに当てはまる変数なので、この式を使うことで「太陽を1つの焦点とするすべての惑星」の運動を記述できるようになる。
運動方程式の極座標表示
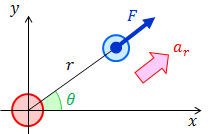
いま、上図のような力がはたらいているとき、r方向の運動方程式は、加速度の成分をarとして、
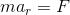
である。
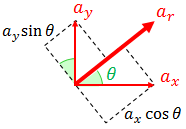
ここで、x, y方向の加速度をax, ayとしてarを表すと
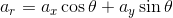
だから、上記の運動方程式は
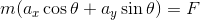
と書き変えることができる。ちなみに、ax, ayは
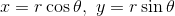
をtで2回微分することで求めることができるので、rおよびθの1回微分、2回微分をそれぞれ
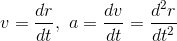
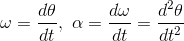
と表記することに決めると、
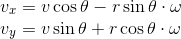
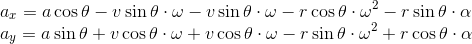
である。よって、
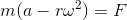
となる。
この式は一般的な場合の運動方程式の極座標表示だが、いま考えているのは惑星の運動なので、楕円の方程式を2回微分することでaを求め、ケプラーの第2法則を用いてrω2を書き変えよう。
楕円の方程式
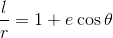
の両辺を1回微分する。
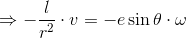
ケプラーの第2法則「r2ω=h」を使ってωを書き変えて
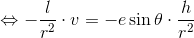
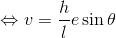
さらに微分する。
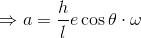
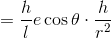
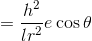
楕円の方程式を使ってe cosθを書き変える。
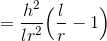
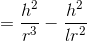
より、
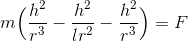
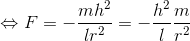
ここでケプラーの第3法則から導いた式を使えば、
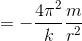
となる。符号が負なのは、引力を表しているから。最後に、円軌道の時と同じように、この力を
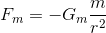
と書き直し、同じ大きさで逆向きの力が太陽にもはたらいているはずだから、その力を
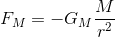
と表すことができる。作用反作用の関係から、これらの力は同じ大きさである。よって、この2式の関係を同時に満たす式は、
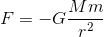
である。これで楕円軌道上を運動する惑星にはたらく万有引力の式が示された。
