ローレンツ力
エルステッドの研究成果を受けて電流と磁場の研究をしていたアンペールは、同じ向きに電流を流した導線は互いに引力を、逆向きに電流を流した導線は互いに斥力を受けていることに気付いた。
電流が磁場から受ける力

アンペールは、1mの導線にはたらく力の大きさが、電流に比例し、導線の間隔に反比例することを発見した。電流をI1,I2,導線の間隔をrとすれば、はたらく力の大きさFは、

で表されることになる。ここで、I1=I2=1〔A〕,r=1〔m〕とすれば、F=2π×10-7〔N〕になることから、1Aの定義が、
- 1m話した1mの導線に2× 10-7Nの力を生じさせる電流
と決定される。

ここで、電流I1が距離rだけ離れた位置につくる磁場の強さは、
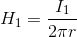
と表されるから、これを用いて力の式を書き変えると、

となる。

この式は、電流I2が磁場H1から受ける力を表していて、それぞれの力の向きは図のようになっている。I2からH1の方へと回転させた右ねじが向かう向きが力の向きなのだ。この関係はベクトルの外積を使って、

と表すことができる。
ここで、
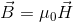
という磁場Hと磁束密度Bの関係を使って上の式を書き変えれば、
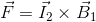
となる。
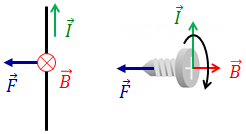
つまり、磁束密度B〔Wb/m2〕の空間の中で1mの導線を流れる電流I〔A〕が受ける力F〔N〕は、外積を用いて
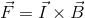
と書けるわけだ。さらに、導線の長さをl〔m〕とすれば、電流が受ける力の大きさはl倍になるはずだから、

になる。この力をアンペール力ともいう。
ローレンツ力
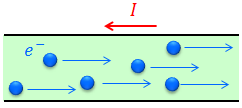
さて、今では電流の正体が電子の流れであることが分かっているので、これを考えることで、運動中の電子が磁場から受ける力を求めることができる。
電流Iの向きと磁束密度Bの向きが直交しているとき、アンペール力Fの大きさは、
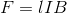
と書くことができる。ここで、電流Iの大きさが「I=envS」と表されたことを思い出すと、この式は
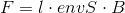
となる。e〔C〕は電気素量、n〔個/m3〕は1m3あたりの電子の個数、v〔m/s〕は電子の速さ、S〔m2〕は導線の断面積である。
すると、いま考えている導線の体積がSl〔m3〕であり、この導線内に含まれる電子の個数Nが

だから、1個の電子が磁場から受ける力の大きさf〔N〕は、
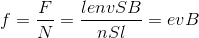
だと分かる。

ただし、気を付けなくてはならないのは、電流の向きと電子の速度の向きが逆だということ。
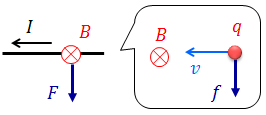
それだと分かりにくいので、電気量+q〔C〕の正電荷の動きを考えると、電流の向きと一致していて分かりやすい。このとき、この荷電粒子が磁場から受ける力の大きさf〔N〕は、
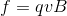
である。q〔C〕の電気量を持つ荷電粒子が磁場から受けるこの力をローレンツ力という。ローレンツ力は、電荷の正負によって向きが変わるので、非常に向きを間違えやすい。そこで、荷電粒子の流れから一度電流の向きをイメージして、F=I×Bで力の向きを確認するようにすれば、間違いは減るはずだ。
一応、ローレンツ力fの向きをベクトルの外積で表せば、
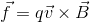
と書けるので、知っておこう。このqは負の値でもいい。
問題
磁束密度Bの一様な磁場を持つ領域に、質量m, 電気量qの荷電粒子を入射したところ、半円を描いてこの領域から出てきた。この荷電粒子が入射されてから出てくるまでの時間tを求めよ。

解答
荷電粒子は領域内で円運動をしていることから、円運動の周期Tを求め、その1/2倍を計算する。
まず、荷電粒子が磁場から受けるローレンツ力の大きさfは、

であるから、円運動の運動方程式は、
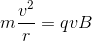
になる。すると角速度ω(=v/r)が
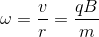
と計算できるので、円運動の周期T(=2π/ω)は

となる。よって、求める時間tは
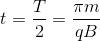
である。
周期Tは荷電粒子の速さvに影響されないのだ。
