三角比
斜方投射のとき、初速度v0を水平成分と鉛直成分に分解しなくてはならないと言った。斜面上の物体に働く力を考えるとき、その力を分解しなくてはならないと言った。今回は、その分速度や分力を角度で表す方法を紹介しよう。
三角比
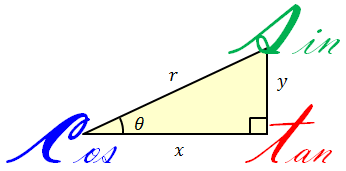
図のような直角三角形を考えたとき、斜辺rに対する対辺yを正弦(サイン)、斜辺rに対する底辺xを余弦(コサイン)、底辺xに対する対辺yを正接(タンジェント)といって、次のように表す。
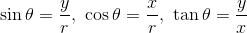
これを三角比という。
今後たくさんの公式が登場することになるが、とりあえず、
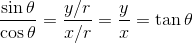
と、
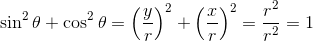
はよく使うので覚えておこう。
また、物理では冒頭でも言ったように、斜辺の長さrが分かっていて、そのほかの長さx,yを利用する状況が非常に多い。その場合は三角比の定義から、
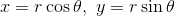
と変形することで利用できる。はじめのうちは、xとyのどちらがsinでどちらがcosなのか迷うと思うが、そのときには定義まで戻って式変形することをお勧めする。徐々に慣れていくはずだ。
練習
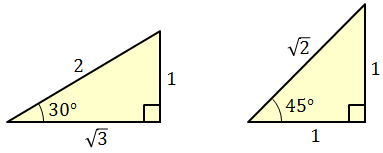
(1) sin30°, cos30°, sin45°, cos45°の値をそれぞれ求めよ。
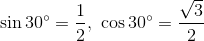
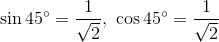
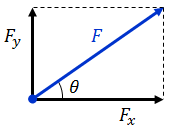
(2) 力Fのx成分Fxとy成分Fyを求めよ。
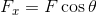
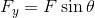
三角関数
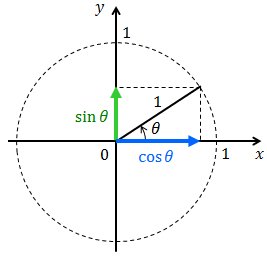
これまでは直角三角形の内角を考えていたのでθは0<θ<90°の範囲しか取り得なかったが、今後はこれを拡張して考えよう。原点を中心とした半径r=1の単位円を考えると、
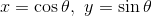
だから、xやyの目盛りがそのままsinθやcosθの値になっていることが分かる。このことから、
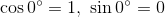
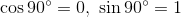
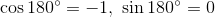
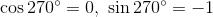
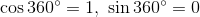
などの値が分かる。このように、三角比を拡張して考えたものを三角関数という。三角関数の大切な性質をまとめておこう。
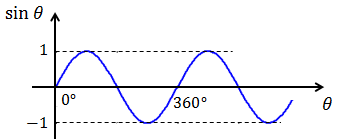
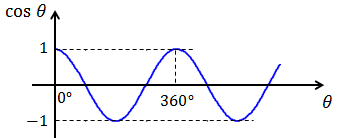
- sinθもcosθも、360°ごとに同じ値になるということ
- sinθもcosθも-1~+1の範囲に収まっているということ。
- sin(-θ)とcos(-θ)が次のように表されること。
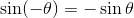
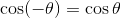
また、sinθ, cosθのグラフは下図のようになる。どちらも360°ごとに同じ値になっており、また、どちらも-1~+1の範囲で振動していることがはっきりと分かる。
加法定理
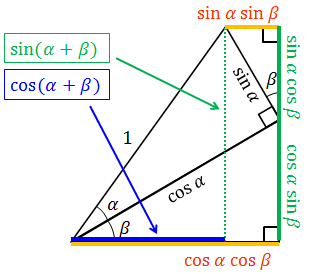
上図より、
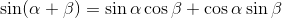
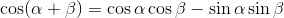
という関係が分かる。これを加法定理という。この図だとα,βが鋭角の場合にしか示せていないが、鈍角の場合にも成り立っている。非常によく出てくる公式なので、暗記してもらって構わない。
次に、加法定理についてα=β=θとすると、
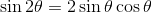
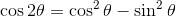
となる。これを倍角の公式とよぶ。
また、cos2θの方の式を「sin2θ+cos2θ=1」を使って書き換えると、
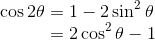
となる。この式から、
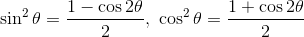
という関係式を作ることもできる。これを半角の公式という。θ→(θ/2)として、
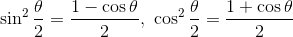
と表した方が分かりやすいかもしれない。倍角の公式や半角の公式は、加法定理から簡単に導くことができるので、無理に覚えようとしなくてもいい。
斜方投射
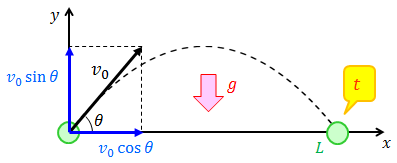
問題
水平面から角度θの向きに初速度v0でボールを投げた。このとき、ボールの水平到達距離Lの最大値および、そのときのθの値を求めよ。重力加速度の大きさをgとする。
→斜方投射の問題。まず、初速度v0を水平成分v_0xと鉛直成分v_0yに分解する。
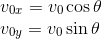
次に、投げられたボールが再び地面に落下するまでの時間tを求める。鉛直方向の運動は鉛直投射と同じだから、等加速度直線運動の変位の式を使って、
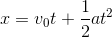
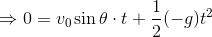
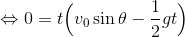
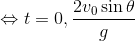
t=0は不適。
また、水平方向の運動は等速直線運動と同じだから、時間tで進む水平到達距離Lを求めると、
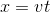

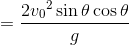
ここで倍角の公式「sin2θ=2sinθcosθ」を使う。
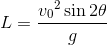
sinθの値は絶対に-1~+1の範囲だから、sin2θ=1のときにLが最大になることが分かる。sin2θ=1になるのは2θ=90°のときだから、Lは
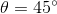
のときに最大値
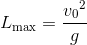
となることが分かる。
