マクスウェル方程式
以前まとめた、静電場・静磁場についての式をもう一度書いておこう。
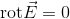

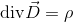

マクスウェル方程式
それでは、電場や磁場が時間変化する場合も含めて成り立つ式を考えてみよう。
まず磁場が時間変化する場合には、電磁誘導の法則より、
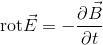
が成り立つ。磁場が時間変化しない場合、右辺は0となって静電場・静磁場の式と同じ式になるので、これを1番目の式と入れ替えてもよさそうだ。
次は2番目の式について考えてみる。両辺のdivをとると、

となるが、左辺は0なので、

となる。しかし、電荷と電流の連続の方程式

があるから、電荷ρが時間変化する場合には2番目の式が成り立たないということになってしまう。この問題を解決するためには、
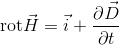
と書きかえる。この式の両辺のdivを取って変形していけば、




となり、電荷と電流の連続方程式を満たすことができるのだ。

以上の内容を踏まえてまとめ直した4種類の式
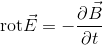
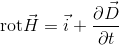
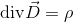
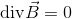
を併せてマクスウェル方程式という。1番目の式は電磁誘導、2番目の式は電流と磁場の関係、3番目と4番目は電荷の存在と単磁荷の不在という電気と磁気の大切な特徴を表している。
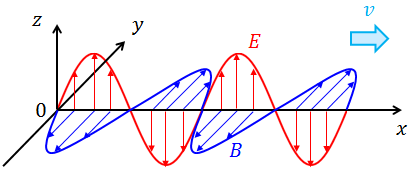
電磁波
電場が磁場を作り、磁場が電場を作る。こうして電磁波と呼ばれる特殊な波は媒質のない真空中も通過することができるわけだ。
マクスウェル方程式を使うと電磁波の様子をイメージすることができるので挑戦してみよう! 計算しにくいので∇を使って書き変えておく。

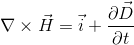


1番目の式のrotを計算すると、左辺は

となる。ここで、
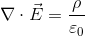
だから、この式は
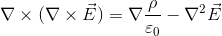
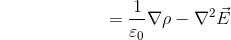
となる。
右辺は、
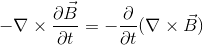
ここで、
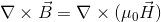


だから、左辺と合わせて
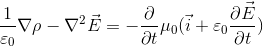
になる。左辺にベクトルEをまとめると、
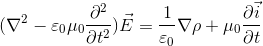
となる。
同じように、マクスウェル方程式の2番目の式のrotを計算すると、左辺は、

である。真空中はdiv H=0だから、
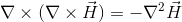
となる。
右辺は、
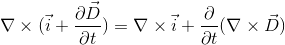
ここで、
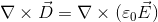

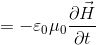
だから、左辺と合わせると、
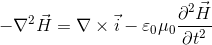
となる。左辺にベクトルHをまとめると、
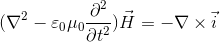
である。
ここで、真空中ではρ=0, i =0だから、導いた2つの式は

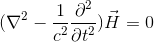
となる。ただし、

である。この形の式を波動方程式という。cは速さ。つまり電場と磁場が真空を伝わる際の速さを示していて、計算すると

となり、光の速さになっている。このことから、光が電磁波の1種であることが分かった。
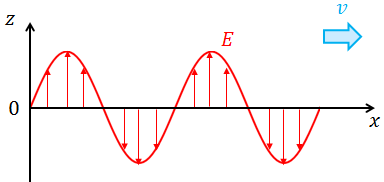
波動方程式を解くと、電場Eと磁場Hの形が求められる。真面目に解くのはやめて、とりあえずEがz成分だけ持つものとしてみよう。つまり、
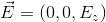
また、これがx軸正の向きに進んでいるとして、
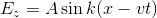
と書くことにする。
ところで、電磁誘導の法則より、
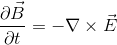
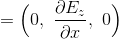
だから、Bはy成分のみを持ち、その値が


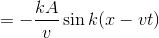
と表されることが分かる。よって、