量子力学

連続固有値 ←→ スピン

　波動関数を時間的、空間的に移動させたとき、対称性からエネルギーや運動量などの保存量が導かれる。今回は回転運動対称性から角運動量を導き、これまでの話には現れなかったスピンと呼ばれる物理量を導出してみよう。

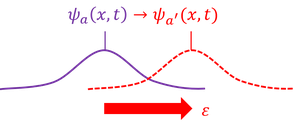
　状態aを表す波動関数Ψをεだけ移動させたとき、この状態a'を表す波動関数は、

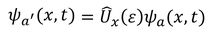
と変換されるとしよう。いま、位置xにおける状態aを表す波動関数と、位置x+εにおける状態a'を表す波動関数が等しい

ことに注意すると、

という関係が得られる。ここで、左辺をテイラー展開すると

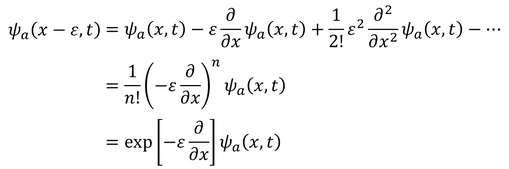
となるから、2式を比較することで、演算子U

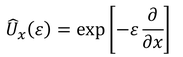
が得られる。また、運動量演算子ｐ

を用いると

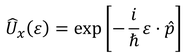
を得る。

　次は、時間をεだけ変化させたときの波動関数を考えよう。

いま、

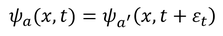
であることを踏まえると

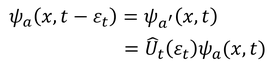
という関係が得られる。ここで、左辺をテイラー展開すると

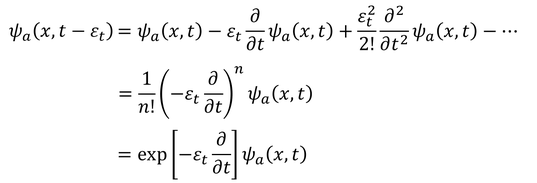
となるから、2式を比較することで、演算子U

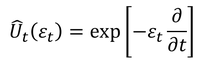
が得られる。また、エネルギー演算子H

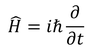
を用いると

を得る。ただし、演算子Uがこのように表せるためには条件がある。

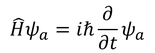
をテイラー展開の式の第3項に使用すると、

となるが、この式が

となる必要があるのだ。そのためには、演算子Hが時間に依存しない量である必要がある。すると

だから、上のようになってくれる。

　次は回転運動を考える。座標がベクトルになっていることに気を付けて、

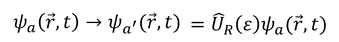
座標の回転を

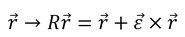
逆回転を

と表す。ここで、回転後の位置における状態a'の波動関数と、回転前の位置における状態aの波動関数が等しい

ことから、

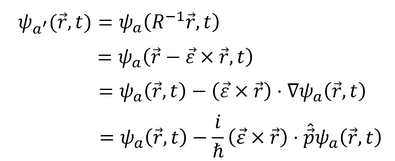
となる。よって、演算子Uが

こうして得られる。L=r×pは水素原子のときにも登場した軌道角運動量演算子である。

　さて、次は波動関数自体がベクトルである場合を考えよう。

すると、座標だけでなく波動関数自体も回転する。

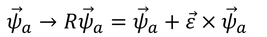
回転した後の位置における状態a'の波動関数を、逆回転させた波動関数が、回転する前の位置における状態aの波動関数と等しい

ことから、

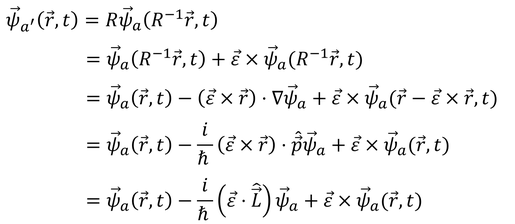
となる。この式は、第3項を除けばスカラー粒子と同じ形になっている。そこで、

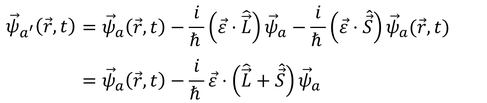
と変形できると考えよう。この演算子Sは、軌道角運動量とは別に、粒子がベクトル粒子であるときに現れるもう1つの角運動量演算子で、スピン角運動量という。

太陽の周りを地球が公転しながら自転しているのと同じく、原子核の周りを電子が公転しながら自転している様子が思い浮かべられてそう名付けられた。ただし、電子が自転しているならば外側の速さが光速を超えてしまうという問題があり、このモデルは正しくないとされている。

　また、原子に磁場をかけると軌道角運動量の影響でスペクトルが分裂する正常ゼーマン効果を以前紹介したが、より詳しく見るとさらに多くの分布が見られる。これはスピン角運動量の影響によるもので、異常ゼーマン効果と呼ばれている。軌道量子数が等しく磁気量子数が異なる状態が縮退している場合、磁場によって縮退が解け、正常ゼーマン効果が表れるのだった。異常ゼーマン効果は、スピン量子数が等しくスピン磁気量子数が異なる状態が縮退している場合、その縮退が解けて現れる現象である。