確率の波
シュレーディンガー方程式によって、物質波の性質が波動関数として表されることが分かった。では、波動関数は物質波の何を表しているのだろうか。
ボルンの確率解釈

2つの隙間が空いたスリットに電子を照射すると、電子はスクリーン上に現れる。どこに現れるかは決まっていないが、試行回数を増やしていくと、光による干渉縞のように、徐々に現れやすい場所と現れにくい場所が交互に並ぶことにな分かれていく。干渉が起こっているということは、1個の電子が2つの隙間を波として通過したことになる。
ではどのような波なのか。電子は波として存在しており、再び現れる場所は確率によって決まっている。つまり、物質波は存在確率の波であるといえるのではないか。ボルンは、波動関数の正体について、次のように考えた。
- 粒子の存在確率は、波動関数の2乗に比例する。
これを「ボルンの確率解釈」という。この考えによると、粒子の位置がx~x+dxの範囲に存在する確率は次のように表される。

一般に波のエネルギーは波の振幅に比例する。エネルギーが大きく密度が大きな場所ほど、存在確率が高くなっている。そう考えると理解はできるだろう。
ここで少し計算の準備を行う。波動関数は複素数なので、その2乗の計算には、複素共役というものを用いる。このとき、

ρを「確率密度」という。
複素共役は、虚数項の符号を反転させたものである。例えば、

という複素数の絶対値の2乗は、

と計算できる。
ところで、-∞~+∞までのすべての確率を足し合わせれば1になるはず。よって、

が成立する。この操作を「規格化」と呼ぶ。
確率密度の流れ

存在確率は、全確率が定数でなければ求めることはできない。普通、規格化は全確率を1とするが、別に2でも100でも構わない。とにかく定数であればよいのだ。では、本当に定数になっているのかを確認しておこう。そのためには、時間微分が0であればよい。



ここで、シュレーディンガー方程式より、


だから、これを用いて


この第1項を部分積分すると、



となり、これは第2項と一致する。ただし、x→±∞における波動関数Ψの値は、確率は0であろうから0とした。よって、

となる。このことから、

であることが分かる。これを1としたものが規格化条件である。
ところで、

を「確率密度の流れ」と呼び、これを用いると、部分積分を実行する直前の式が、


となるので、

という関係式が得られる。これを「連続の方程式」と呼ぶ。電磁気のときに学んだ、電流に関する連続の方程式

と同じ形であることから、確率密度が時間変化している様子がイメージできる。ただし、全確率は1である。
期待値

では、位置xや運動量pはどの値を取りやすいのか。ここでは期待値を求めてみよう。期待値は試行回数を重ねた場合の平均値のことで、考えられる状況とその確率との積を、状況の数だけ足し合わせることで求めることができる。よって、位置xの期待値は、

と表すことができる。
では、運動量pの期待値を求めてみよう。位置xの期待値を時間tで微分することで計算できる。


ここで、シュレーディンガー方程式を用いると、



となる。
ここで第1項を部分積分すると、



となるので、これを元の式へ戻すと、



となる。このことから、運動量の期待値は、演算子を用いて

と書けることが分かった。
エーレンフェストの定理
最後に、運動量の期待値を時間微分してみよう。


第2項の偏微分を前後入れ替えて、

シュレーディンガー方程式を用いる。



第1項は部分積分によって、



第2項と一致することが分かる。よって、



-dV/dxの期待値となる。これは、保存力である。つまり、
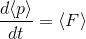
が成り立っていることになる。ニュートンの運動方程式だ。こうして、ミクロな世界とマクロな世界が、こうして期待値によってつながっているということなのだ。この関係を「エーレンフェストの定理」という。
