物質波
ボーアは量子条件と振動数条件という2種類の仮説から出発し、新たな原子モデルを導き出した。これにより、ラザフォードのモデルでは説明できなかった問題を解決することができた。次の課題は、どうしてそのような仮説が成り立つのかである。
物質波

アインシュタインの光量子仮説によれば、光は、エネルギーE=hν,運動量p=h/λを持った光子の集まりであるらしい。それまで波だと思われていた光に粒子性があるならば、これまで粒子と思われている電子には波動性があるのではないか。このような考えに至ったのは、ルイ・ド・ブロイである。彼は、光量子仮説による運動量の式を
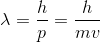
と書き変え、あらゆる物質は波動性を持つとした。この波を「物質波(ドブロイ波)」、この波長を「ドブロイ波長」という。特に、電子の物質波を「電子波」という。あらゆる物質が波動性を示すとはいっても、プランク定数hがかかっていることからも分かるように、その波長は極めて小さい。具体的に計算してみると、40m/sで運動しているボールのドブロイ波長は、約1.1×10^(-34)mになる。よって、マクロな世界において、波動性が現れる場面はないといってよい。しかし、例えば100Vで加速された電子のドブロイ波長は、約1.2×10^(-10)mと、原子の大きさや結晶の格子間隔とほぼ一致するため、ミクロな世界では無視できない大きさとなる。
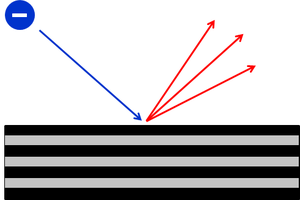
デビッソンとガーマーは、電子をニッケルの結晶に照射する実験を行ったところ、散乱角度によって、強度が強くなったり弱くなったりしていることを発見した。これにより、電子が波として回折と干渉を起こしていることが確かめられた。この実験を「電子回折」という。
波束

物質波とは一体何か。試しに音のうなりを思い出してみよう。うなりは、わずかに異なった振動数の音が重なり合って、音が大きくなったり小さくなったりして聞こえる現象だ。

うなりの振動数と同じように、わずかに波長の異なった波が重なり合うと、やはり波のかたまりができる。これを「波束」と呼ぶ。波束を遠目に見ると、粒子のように見えないだろうか。ひとまず、粒子はこのような波束の状態で存在していると考えることにしておこう。
ところで、この波束は、大きなかたまりの部分と、このかたまりを作り出している細かな波の部分とで構成されている。細かい方の速度を「位相速度」、大きなかたまりの部分の速度を「群速度」という。位相速度は、波の基本式
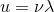
で表される。
群速度も求めてみよう。例えば、わずかに波長と振動数の異なる次のような2つの波
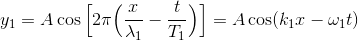
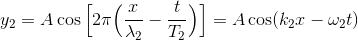
を考えて、足し合わせてみる。すると、
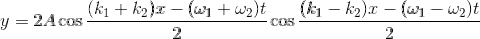
となる。前半のcos成分は、細かい波の振動の方を表しており、後半部分のcos成分が、大きなかたまりの部分の形を表している。つまり、後半部分の時間変化が群速度というわけだ。だから、この成分の値が一定となる位置(例えば頂点)
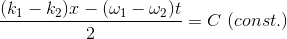
の時間変化を考えればよい。よって、
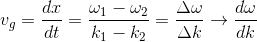
で求められることがわかる。ωは「角振動数」、kは「波数」という。
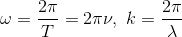
では、群速度を求めるために、物質波におけるωとkの関係を見つけよう。例えば、粒子のエネルギーは

と表されるが、ドブロイはあらゆる粒子に波動性があると考えたのだから、この式へ光子のエネルギーと運動量の式を代入してみる。
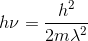
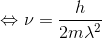
すると、νはωに、λはkに直せるから、
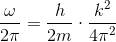

が導出できる。このような、ωとkの関係を「分散関係」と呼ぶ。それでは群速度を求めよう。
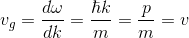
すると、粒子の速度と一致することが分かる。このことから、粒子が波束の状態で存在しているということが予想される。
量子条件
ではボーアの量子条件に話を戻そう。実は、

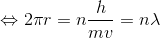
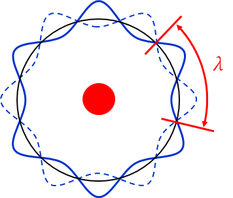
こうして書き変えてみると分かるように、この式にはドブロイ波長が含まれていたのだ。左辺は半径rの円周の長さだからつまり、
- 半径rの円周の長さが、ちょうど波長の整数倍になるような軌道にしか電子は存在することができない。
ということを、量子条件は表していたのである。つまり定常状態とは、電子が定常波になっている状態のことだったのだ。

ところで、ボーアの量子条件の左辺は円周の長さであるが、これは楕円にも拡張することができて、

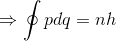
この関係を「ボーア・ゾンマーフェルトの量子条件」と呼ぶ。この条件を使って、単振動について詳しく考えてみる。単振動のエネルギーは、

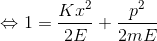
となり、この式は、p-xグラフ上で楕円を描くことが分かる。ボーア・ゾンマーフェルトの量子条件の左辺は、このグラフで囲まれた面積を表しているので、これを計算すると、

よって、

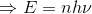
となる。これは、プランクの量子仮説である。電磁波のエネルギーの式が、振動する粒子のエネルギーとしてこうして一般化されたということになる。
