水素原子r
これまで、水素原子のシュレーディンガー方程式について、φの解とθの解を見てきた。今回は、最後に残ったrの解について考えていこう。
rが非常に大きいとき

前回、λをl(l+1)で書き変えたので、rの方程式もlで書き変えることにする。また、ポテンシャルV(r)を水素原子のポテンシャルで表す。すると、シュレーディンガー方程式は、
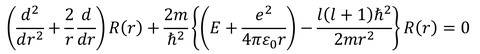
となる。
一般的な解を紹介する前に、だいたいの傾向をつかんでもらいたいので、rが非常に大きいときと、rが0に近いときの解を考えてみる。まず、rが非常に大きいときは、分母にrを持つ項を無視できるから、

となる。ここで、E<0に注意して

とおくと、

となる。この方程式の特解は、
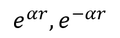
であるが、r→∞のとき、波動関数は0になって欲しいから、
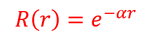
を選択しよう。グラフは下図。

rが0に近いとき
rが0に近いときのシュレーディンガー方程式は、微分の項と、分母にr^2がある最後の項だけを残そう。すると、
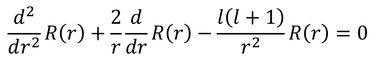
となる。ここで、
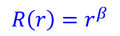
とおくと、
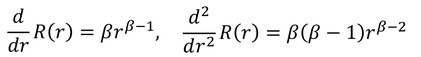
だから、これらを元の式に戻すことで、
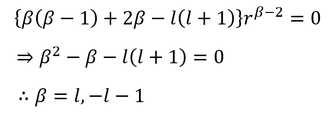
βが2つ得られる。ここでは、r→0のときに波動関数が無限大になってほしくないので、β=lを選択する。よって、

となる。グラフは下図(l≠0)。

rが非常に大きいときと、0に近いときの解を組み合わせて、

これを元のシュレーディンガー方程式の1つの解と考えてみよう。グラフは下図のようになる。

なんだかいい感じがする。では、この式を元の方程式に当てはめて、妥当かどうかを検討しよう。
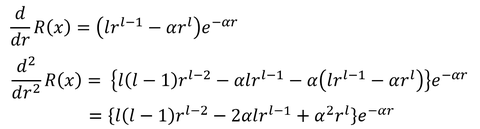
より、
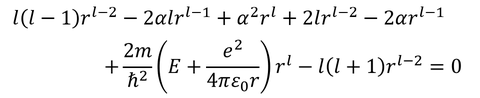
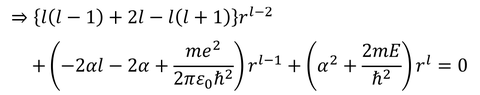
ここで、
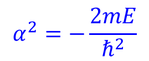
より


を得る。ただし、n=l+1とした。この結果は、ボーアの原子モデルのところで紹介した、エネルギー準位になっている。また、ここで使われている整数n=1,2,3…を、主量子数と呼んだことも思い出そう。
では、このグラフのピーク時のrの値が、ボーアの理論による軌道半径rと一致するのかどうか考えてみよう。微分が0になるという条件から、
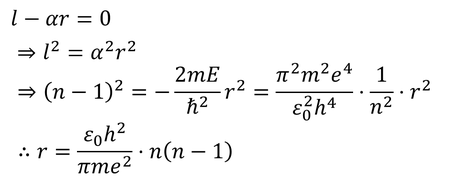
が得られるが、これは、ボーアの理論のところで導いた軌道半径とは異なる。どうしてだろう?
r方向の存在確率
波動関数uの規格化条件に注目してみよう。これを極座標で書き変えると、

となる。ここで、uをRとYに分離してやると、
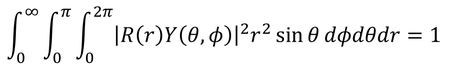
となるが、Yが次のように規格化されているとき、
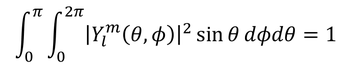
Yを球面調和関数と呼んだ。いまの式変形でもこの関係が成り立っているとしよう。すると、

となる。ここで、新しい波動関数

を考えると、新しい規格化条件
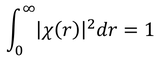
を得る。χ(r)のグラフはR(r)のグラフと似た形になるが、ピーク部分のrを求めておこう。微分が0になるという条件から、
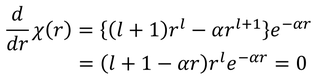
α,l,Eをnで表せば、

を得る。ボーアの理論のところで導出した軌道半径と一致する。どうやら、
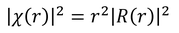
がr方向の存在確率を表していいると考えてよさそうだ。
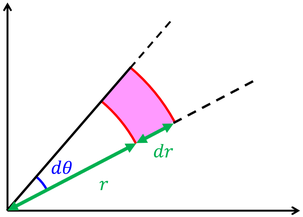
どうして存在確率がr^2に比例するのかというと、中心からの距離rが長いほど、dθやdφの角度に対する体積が大きくなるので、球の表面積に存在確率が比例するというわけだ。
ラゲールの陪多項式
一般的に、元の方程式の解は

と表せる。r_0はn=0のときの軌道半径で、ボーア半径という。

また、L(x)はラゲールの陪多項式と呼ばれ、

と表される。ただし、0≦j≦kである。この大小関係から、
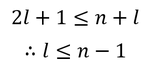
軌道量子数(方位量子数ともいう)lと主量子数nのあいだに、このような関係があることが分かる。前回登場した磁気量子数mとlの関係も含めてまとめると、次のようになる。
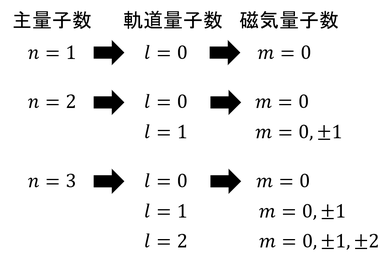
n=1のときは1種類の状態しか取れないが、n=2のときは4種類、n=3のときは9種類の状態を取ることができる。これらを「4重に縮退している」「9重に縮退している」と表現する。
それでは最後に、いくつか存在確率|χ(r)|^2を求めよう。
① 1s軌道(n=1,l=0)

② 2s軌道(n=2,l=0)
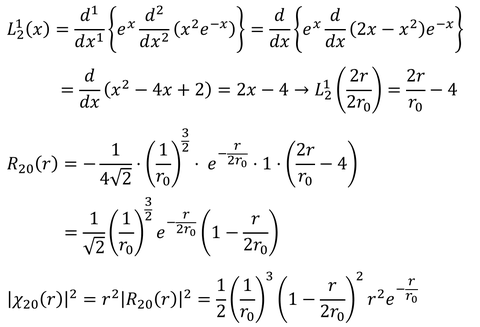
③ 2p軌道(n=2,l=1)
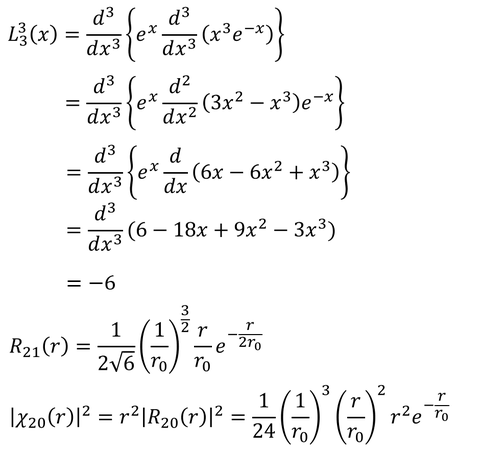
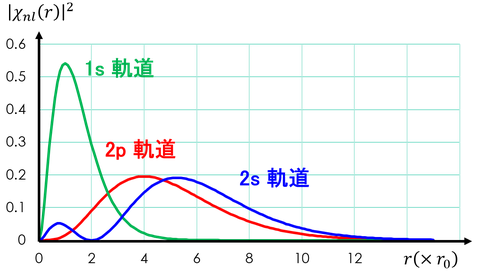
計算した確率分布をグラフに表すと上図のようになる。横軸はボーア半径の何倍かを表している。1s軌道のピークがちょうどボーア半径と等しくなっており、2p軌道のピークはちょうどボーア半径の4倍(=2^2倍)になっていることがわかる。また、2s軌道は山が二つあり、小さい方はボーア半径よりも小さな位置がピークになっている。
以上、3回にわたって、水素原子に含まれる電子の存在確率を求めてきた。電子が確率の波として原子核の周囲にぼんやりと存在している様子がイメージできるようになっただろうか。この電子の様子を、「電子雲」と呼ぶこともある。
