水素原子φ
水素原子は、1個の陽子の周囲に電子が1個だけ存在するもっとも単純な構造の原子だ。ところが、意外とその構造は複雑でだったりする。今回から数回に分け、この電子の存在確率と、水素原子の構造について議論を重ねてていこう。
水素原子のシュレーディンガー方程式

水素原子に含まれる電子は、中心からの距離rに依存するポテンシャル
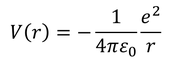
を持っている。符号がマイナスなのは、源となる力が引力だからである。そして、このポテンシャルを含んだシュレーディンガー方程式を解くことで、電子の存在確率を求めることができる。ただ、これまでに考えた井戸型ポテンシャルや箱型ポテンシャルの問題は1次元の運動だったが、今回は3次元の運動なので、

このようになる。∇^2はラプラシアンである。ここで、ポテンシャルは距離rによって決まる球対称な分布をしているから、シュレーディンガー方程式の変数は、ⅹ,y,zの直交座標よりもr,θ,φの極座標の方が性質が考えやすいだろう。そこで、シュレーディンガー方程式を極座標形式で書き変える。

ラプラシアン中のθとφの部分をまとめてΛ(θ,φ)と書いた。
変数分離
このままでは解けないので、波動関数u(r,θ,φ)が、それぞれの変数を持った部分に分けられるとして変形していく。つまり、
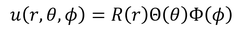
のように表せるとして、方程式を変形する。ただ、いきなり3つに分類はできないので、まずは
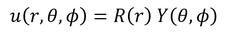
のように、rの部分とそれ以外の部分に分けて考えることにしよう。これをシュレーディンガー方程式に代入すると、

となる。Λ(θ,φ)の項を右辺に持ってきて、

両辺をRYで割る。

これで、左辺にrのみを、右辺にθとφのみを変数にもつ部分に分けることができた。すると、両辺は定数でなければならないので、これをλと表すことにする。以上より、
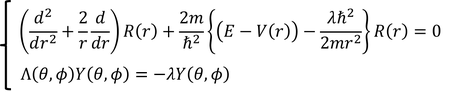
シュレーディンガー方程式を、rの式とそれ以外の変数の式に分離することができた。
続いて、Y(θ,φ)を
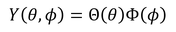
とおき、θとφの式へ代入する。

両辺にsinθの2乗を掛け、
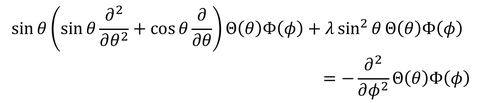
ΘΦで割る。
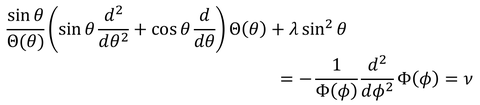
これで左辺にθ、右辺にφと分けることができた。両辺は定数でなければならないからこれをνとおく。これで、
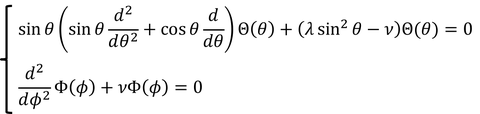
θの式と、φの式を得ることができた。
まとめ
① rの式

② θの式

③ φの式

φの解
では、作った方程式を順番に解いていこう。まずは一番簡単そうなφの式(③)を解く。この式は、

と書けば分かるように、一般解
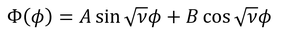
を持つ波である。ただしφ方向の波なので、ぐるりと一周する波である。

また、この式の一般解は
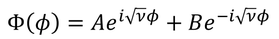
とも書ける。第1項と第2項は、それぞれ逆回りの波を表しているわけだが、今は波の形にしか興味がないので、そのうち一方
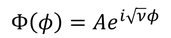
を解として採用しよう。
ここで、この波はぐるりと一周しているわけだから、φ=0のときとφ=2πのときとで波動関数が一致していなけれあならない。

このことから、
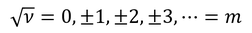
√νが整数でなければならないことが分かる。これをmと置こう。※電子の質量と同じ文字を使うが、別ものである。
境界条件を考えたが定数Aが定まらなかった。そこで、規格化条件を考えよう。φ=0~2π範囲に電子は必ずいるはずだから、積分範囲をそのように取る。

これでAが定まった。以上より、φ方向の解
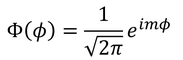
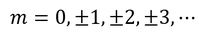
が得られた。
