水素原子θ
前回は水素原子のシュレーディンガー方程式を極座標形式で表し、それをr,θ,φの式へ分離した。今回は、θの式に注目し、

θの解を求めよう。
特殊解
はじめに上の方程式を満たす特殊解を4つ紹介する。具体例を見ながら、その傾向をつかもう。
① Θ=C(定数)
定数Cを上の式へ代入すると、

となり、この式が恒等的に成り立つには、
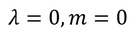
でなければならないことが分かる。
② Θ(θ)=cosθ
cosθを上の式へ代入すると、

となり、
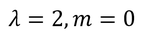
でなければならないことが分かる。
③ Θ(θ)=sinθ
sinθを上の式へ代入すると、
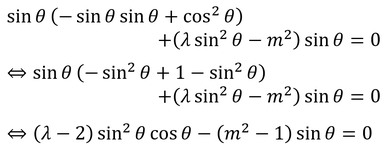
よって、
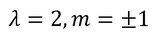
でなければならないことが分かる。
④ Θ(θ)=sin2θ
sin2θを上の式へ代入すると、

よって、
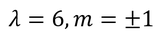
でなければならないことが分かる。
以上の結果をまとめると、

このようになる。結論から言えば、λも実は整数の値しか取らず、0,2,6,12,…と増えていく。そして、この値は、整数l=0,1,2,…を使って、
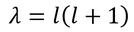
と表すことができる。ここで、lは「軌道量子数」、mは「磁気量子数」と呼ばれている。以降はλをlで表す。
ルジャンドルの陪多項式
もとのθの式を(sinθ)^2で割り、λをl(l+1)と書き変えると次のようになる。

ここで、
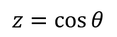
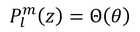
とおくと、

となる。ただし、
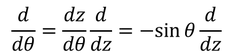
を用いた。
ここで、m=0のとき、
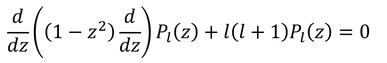
これを「ルジャンドルの微分方程式」と呼び、この解P(z)を「ルジャンドルの多項式」と呼ぶ。ルジャンドルの多項式はロドリグの公式によって、

と表されることが知られている。具体的にl=0,1,2について計算してみれば、

となる。
ルジャンドルの多項式を用いて、元の方程式の解は、
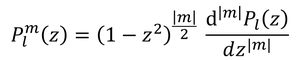
と表せる。これを「ルジャンドルの陪多項式」と呼ぶ。具体的にl=0,1,2について計算してみると、

となる。ここで、ルジャンドルの多項式はzのl次式であり、ルジャンドルの陪多項式は、それをm回微分しているから、mが満たす条件
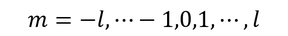
が得られる。つまり、l=2のとき、mは-2,-1,0,1,2の5つの整数しか取ることができない。
球面調和関数
角度θ方向の電子の存在確率は|Θ(θ)|^2によって得られる。せっかくなので、これに前回の結果Φ(φ)を加えて、全方位の存在確率を求めてみよう。前回、ΘとΦの積を

と置いていたから、これを用いる。Θ(θ)をP(cosθ)と書き変え、Φ(φ)は前回求めた結果を使うと、
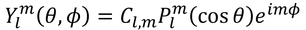
となる。CはΘとΦの係数をまとめたもので、規格化することで定まる。
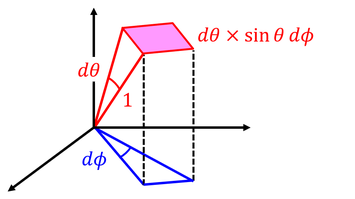
規格化条件の式は、電子がdθdφのあいだに収まる確率

を球面全体で足し合わせればいいから、
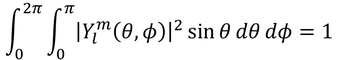
となる。こうして規格化されたY(θ,Φ)を「球面調和関数」という。では、いくつかの球面調和関数と、それを2乗した電子の存在確率の分布を見てみよう。




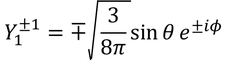
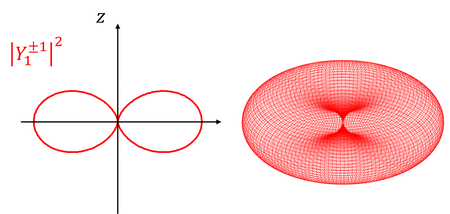

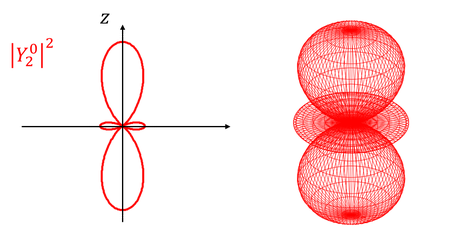

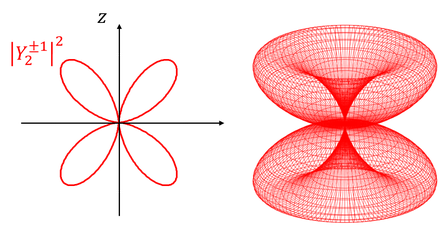

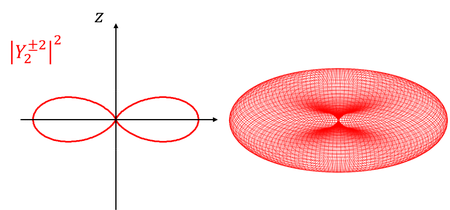
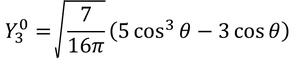
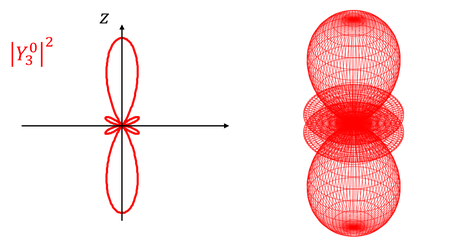
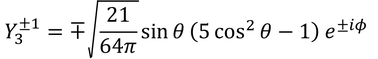
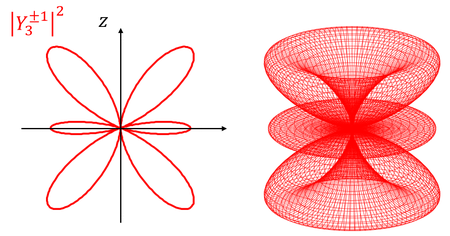


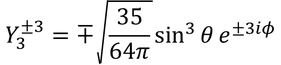
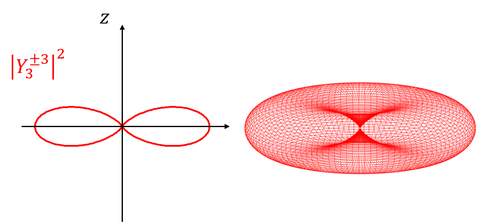

l=0のときの電子の位置をs軌道、l=1のときをp軌道、l=2のときをd軌道、l=3のときをf軌道と呼ぶ。それぞれ、sharp鋭い)、principal(主要な)、diffuse(広がった)、fundamental(基本的な)の頭文字らしい。ちなみにl=4以降は、g軌道、h軌道、…となっていく。
