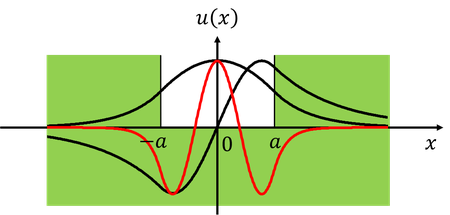
有限の井戸
前回は無限大のポテンシャルに捕らわれた粒子について考えた。今度は、有限の値を持つポテンシャルを考え、量子の性質をより深く考えていこう。
有限の深さの井戸型ポテンシャル
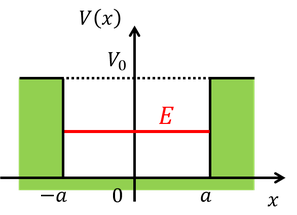
x=-a~aポテンシャルが0で、その外側がV_0であるような井戸型ポテンシャルに、エネルギーEを持った粒子が閉じ込められているとしよう。E<V_0のとき、古典的な粒子であれば、粒子はこの井戸から外へ出ていくことはできない。しかし、量子力学として考えると、実はわずかに井戸の外へ染み出すことができるのだ。存在確率が0ではないということは、波動関数が0ではないということだ。そこで、井戸の内側と外側で場合分けをして考える必要がある。それぞれシュレーディンガー方程式を立ててみよう。
①井戸の内側(-a<x<a)
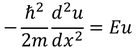
②井戸の外側(x<-a,a<x)
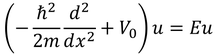
これらを解いていく。
①は、
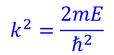
とすれば、
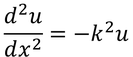
となるから、一般解

が得られる。
②は、
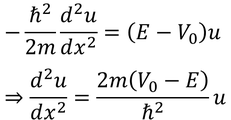
より、

とおけば、
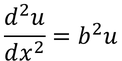
となるから、一般解

が得られる。
ここで、x→±∞のとき、u→0としよう。xが-∞のとき、e^(-bx)は無限大に発散してしまうので、波動関数uが0に収束するためには、D=0でなければならない。よって、
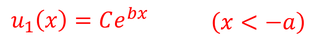
となる。xが+∞のときは、e^(bx)が無限大に発散してしまうので、uが0に収束するためには、C=0でなければならない。よって

パリティ
一般に、ポテンシャルの形が偶関数で表されるとき、その波動関数は偶関数、または奇関数となる。説明してみよう。
まず、xについてのシュレーディンガー方程式
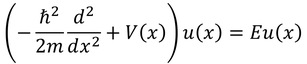
と、-xについてのシュレーディンガー方程式
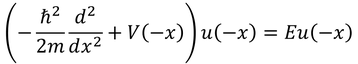
を立てる。いま、ポテンシャルが偶関数であれば、V(-x)はV(x)と等しいから、
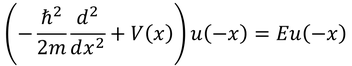
となる。この式とxについてのシュレーディンガー方程式を比較すると、演算子が等しく、同一の固有値だから、対応する固有関数も同じものであることが分かる。固有関数が同じであるとは、規格化すると等しくなるということだから、定数cを使って
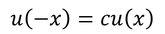
と書ける。この式は、xの符号を反転させると、元の関数のc倍になっていることを表している。ここで、もう一度反転させると、

よって、c=±1
このことから、許される波動関数が、

であることが分かる。ここで、波動関数が偶関数のとき、波動関数は「正のパリティを持つ」といい、奇関数のとき、波動関数は「負のパリティを持つ」という。
固有関数
波動関数が正のパリティを持つとき、
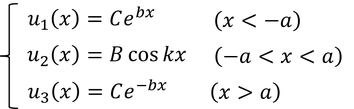
全体が偶関数であることから、x>aのときの波動関数の係数DにCと書き変えている。ここで、境界条件として井戸の両端で波動関数がなめらかにつながるという条件を加えよう。まず、u2とu3を微分して、
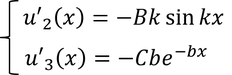
これらより、x=aについて、境界条件
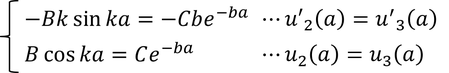
を得る。この2式から

という、baとkaの関係式が得られる。
また、k^2の式とb^2の式より、
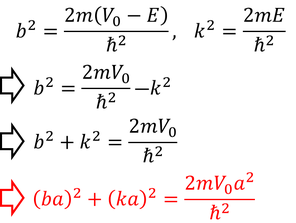
2つめのbaとkaの関係式が得られる。この2式を解くことで、固有関数を求めることができるが、難しいので、2種類のグラフを書いて、その交点を調べてみよう。

円の半径Rは
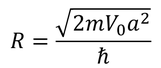
である。Rが大きいほど交点が増える。つまり、V_0やaが大きいほど、固有状態の数が増えるということが分かる。
続いて波動関数が負のパリティを持つときは
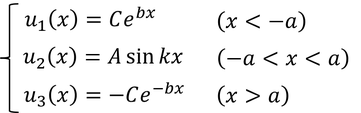
である。u3の係数Dは、全体が奇関数であることから-Cとした。井戸の端における境界条件は、u2とu3の微分
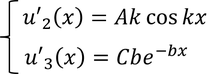
を考えて、
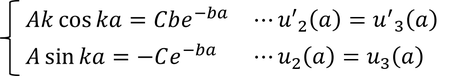
となる。これらより、

という関係が得られる。コタンジェントcotはtanの逆数。
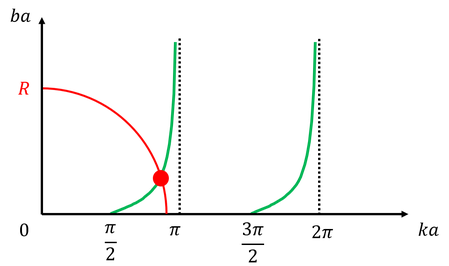
今度も、Rが大きいほど、固有状態の数が増えることが分かる。
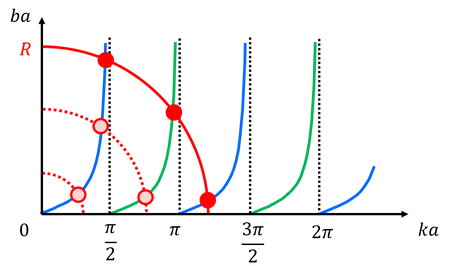
まとめるとこのようになる。このことから、Rがπ/2よりも小さいときは固有状態は1つであり、そこからπ/2大きくなるごとに固有状態の数が1つずつ増えていくことが分かる。いくつか、Rの大きさごとの波動関数を書いてみると、次のようになる。
①0<R<π/2
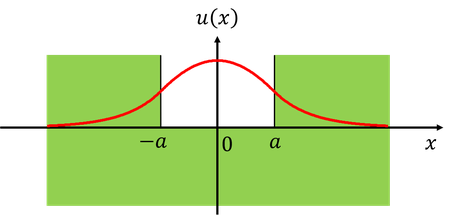
②π/2<R<π
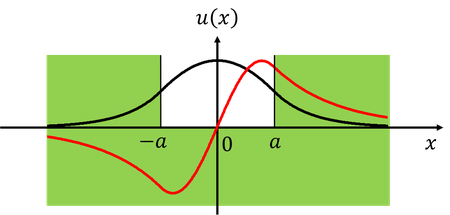
③π<R<3π/2