量子力学

シュテファン・ボルツマンの法則　←→　光の運動量

　プランクの量子仮説によると、「電磁波のエネルギーはとびとびの値を持つ」。これは何を意味しているのだろうか。

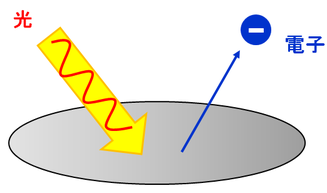
　ピカピカに磨いた金属に紫外線などの光（電磁波）を当てると、電子が飛び出してくることがある。この現象を「光電効果」、飛び出す電子を「光電子」という。この現象について詳しく調べてみると、次のようなことが分かってきた。

1. 強い光でも光電子が飛び出してこないことがある。
2. 弱い光でも光電子が飛び出してくることがある。
3. 光電子の運動エネルギーは、光の振動数が大きいほど大きくなる。
4. 光を強くすると、光電子の数が増える。

　一般的に、波のエネルギーはその振幅の2乗に比例して大きくなるので、強い光、振幅の大きな光ほど大きなエネルギーを持っているはずである。ところが、1番2番から、光電子が飛び出してくるかどうかは、波のエネルギーに関係がないようだ。では何に関係しているかというと、振動数である。光の振動数が大きければ、弱い光でも光電子は飛び出し、振動数が小さければ、強い光でも光電子は飛び出してこないのだ。光電子が飛び出すギリギリの振動数を、「限界振動数」という。この事実を受けて、アインシュタインは次のように考えた。

• 光はエネルギー「ε=hν」を持った粒子の集まりである。

この考えを「光量子仮説」といい、光の粒子を「光子」という。光を波と考えた場合、金属内の電子を振動させるだけで、電子を飛び出させることはできないが、光を粒子と考えれば、金属内の電子を弾き飛ばせると考えたわけだ。また、1個の光子のエネルギーを

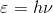
と考えれば、光子の集まりである電磁波のエネルギーが、

というプランクの量子仮説を満たすことが理解できる。

　では光が波動であるという考えは誤りなのかというとそうではない。アインシュタインは、光は粒子性と波動性の両方の性質を併せ持っていて、どちらの性質が現れるかはそのときの状況によると考えた。この考えを「粒子と波動のに二重性」という。

　続いて光電子のエネルギーに注目してみよう。光の振動数を変えながら光電子のエネルギーの最大値を測定すると、上のようなグラフが得られる。グラフが横軸と交わる点ν_0が限界振動数である。また、この直線は、傾きをh，切片を－Wとすると、

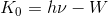
と表すことができる。傾きhは、これまでに何度も登場した定数で、これを「プランク定数」という。プランク定数はこのような実験により、ミリカンによって求められた。

式の中に含まれるhνは光子のエネルギーであり、K_0は光電子のエネルギーの最大値だから、Wは金属内の電子を金属の表面まで運ぶのに必要な最小エネルギーとなっている。これを「仕事関数」という。

と考えるとイメージしやすい。光子が持つエネルギーhνの一部Wを金属内の電子が受け取り、残りのエネルギーK_0を持った光電子が飛び出してくるというわけだ。光電子が持つエネルギーが0となる場合は、

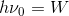
という関係が成り立っており、このときの光の振動数ν_0が限界振動数である。

　このように、光の振動数によって飛び出す光電子の運動エネルギーが変化するわけだが、振動数を変えずに強い光に変えると、今度は光電子の数が増える。これは、電子と衝突する光子の数が増えたためであると考えることができる。