ブラ・ケット
波動関数の2乗が粒子の存在確率を表し、演算子で表された物理量をかけ合わせることで、その物理量の期待値を得ることができる。

また、演算子を適切な波動関数に掛けることで、その物理量の固有値を得ることができる。
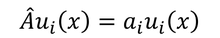
この式を「固有値方程式」と呼び、波動関数を「固有関数」と呼んだ。
正規直交完全系
複数の固有関数の足し合わせで任意の波動関数が表現できるとき、一連の固有関数を「完全系」と呼ぶ。

固有関数の間に
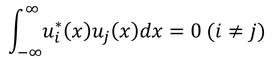
という関係があるとき、これらは互いに「直交系」をなすという。また、
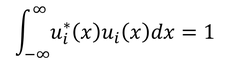
という制約を課すことを「規格化」と呼ぶ。規格化された直交完全系のことを「正規直交完全系」と呼ぶ。直交系の条件と規格化の式は、まとめて
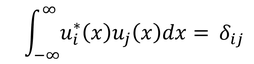
と表すことができる。δはクロネッカーのデルタと呼ばれ、i=jのときは1,i≠Jのときは0を取る。
ここで、
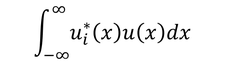
という式を考えよう。この式のu(x)へ、固有関数を使って展開した式を代入して計算すると、

となる。つまり、与えた式は展開係数cなのである。
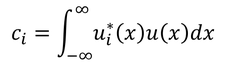
この係数cを元の展開式へ代入すると、
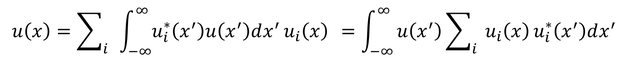
となる。
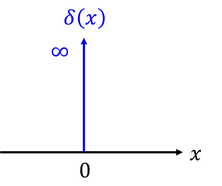
ここで、x=0のときだけ無限大の値を取り、そのほかのxのときは0という関数δ(x)を導入する。これを「デルタ関数」という。デルタ関数は、全範囲で積分すると1になる

と決められているので、
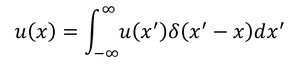
という関係が成り立つ。これを、波動関数の展開式と比較することで、

を得る。この関係は、展開に使用した固有関数が完全系をなしている場合に成立する「完全性の条件」である。
状態ベクトル
任意の波動関数が正規直交完全系をなす固有関数の組み合わせで表されるとき、波動関数の状態を決めているのは展開係数であることが分かる。そこで、展開係数cを順番に並べたベクトルを考え、
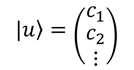
これを「状態ベクトル」と呼ぶ。さらに、この状態ベクトルの共役を取り、横に並べ直したベクトル
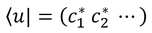
を考えると、この内積は
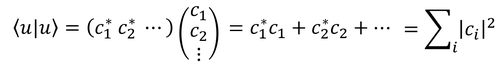
と表すことができる。特に、<u|を「ブラベクトル」、|u>を「ケットベクトル」と呼ぶ。この記号を用いることで、ベクトルの内積を括弧(ブラケット)で表現できるのだ。
では、ブラ・ケットを使ってこれまでにまとめた式を書き直してみよう。波動関数u(x)の複素共役

を考えると、任意の波動関数の規格化条件
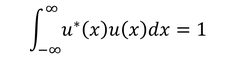
の左辺は
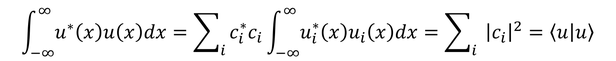
になる。途中で固有関数の規格化条件を使った。よって、任意の波動関数の規格化条件をブラケットを用いて表せることがわかった。

また、2種類の波動関数を
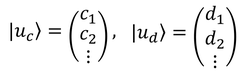
と表すと、この内積は
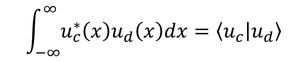
となる。
期待値はu*とAuの内積だから、この関係が使えて、
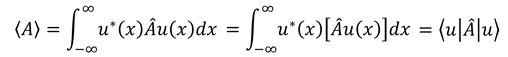
と表すことができる。
基底ベクトル
任意の波動関数が展開係数で表せるのだから、それぞれの固有関数も同様に展開できる。固有値方程式を

と表したとき、|u_i>を「固有ベクトル」と呼ぶ。固有ベクトルを使って任意の状態ベクトルを展開することもできて、

固有ベクトルがそれぞれ正規直交完全系をなすとき、これらを「基底ベクトル」という。
固有ベクトルが正規直交関係を満たすためには、内積がクロネッカーのデルタになればよい。

次は固有ベクトルが完全性を満たす条件を考える。展開係数cが

と表せるので、これを展開式へ戻すと、

となる。これより、

を満たす必要があることが分かる。これが完全性の条件である。
エルミート行列
ブラベクトルとケットベクトルの積は定数になった。しかし、完全性の条件にあるようにケットベクトルとブラベクトルの積の場合は定数にはならず、縦と横の数が等しい「正方行列」になる。左辺が正方行列なら右辺の1も実は正方行列になっていて、これを「単位行列」という。単位行列は、対角成分がすべて1で、そのほかの成分がすべて0の行列である。

同じように、物理量を表す演算子も正方行列で表すことができて、

すると固有値方程式は、

のようになる。
では、演算子Aの成分を求めよう。状態ベクトルに演算子Aを掛けたベクトルを考える。
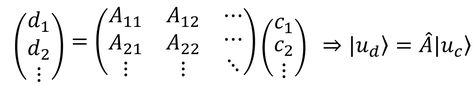
新しい状態ベクトルの成分は、
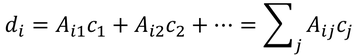
であるが、展開係数の式から

と表すこともできる。ここで、
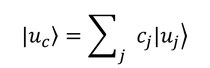
と展開すれば、

という関係を得る。よって、演算子を表す行列の成分が、
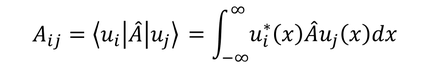
であることが分かる。
ここで、この成分の行と列を入れ替え、複素共役を取った行列を「エルミート共役な行列」という。その成分は、

である。元の行列とエルミート共役な行列が等しいとき、

この行列を「エルミート行列」という。
