トンネル効果
ポテンシャルが有限の値であるとき、波動関数はその内部に染み出すことが許される。その結果、量子力学の世界では、ポテンシャルの壁を粒子が通り抜けるという現象が起こる。これを「トンネル効果」という。
箱型ポテンシャル

図のようなポテンシャルを考え、この箱型ポテンシャルに、エネルギーE(<V_0)を持った粒子が左側からやってきたとする。この粒子が箱を通過する確率(透過率)を求めてみよう。
今回も波動関数がxの部分とtの部分に分けられるとすると、時間に依存しないシュレーディンガー方程式は、

となる。前回と同じk,bを用いて、①の一般解を、
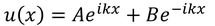
②の一般解を、

と表す。

①の一般解の、Aの項は、波動関数f(t)と組み合わせると
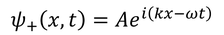
となり、x軸正の向きに進む波を表していることが分かる。同様にBの項は、

となり、x軸負の向きに進む波を表していることが分かる。x<0の位置では、粒子はこの2つの波の重ね合わせで存在しているわけだ。この粒子の向きを考えると、x>aの部分では粒子は正の向きにしか進まないはずだから、この位置での波動関数を、
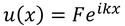
と表すことができる。
まとめ
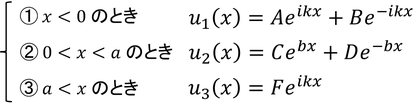
透過率
このポテンシャルを通過し、x>aの位置に粒子が存在する確率は、波動関数の2乗
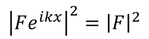
に比例している。同様に、x<0の位置を正の向きに進む粒子の存在確率は、
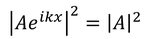
に比例している。このことから、粒子の透過率は、

と表されることになる。では、これを求めよう。
透過率を求めるためには、3種類の波動関数u1,u2,u3に使われている係数A~Fが分かればいい。そこで、箱の境界(x=0,a)で波動関数がなめらかにつながるという境界条件を考える。すると、微分を用いて、次の4種類の関係式が得られる。
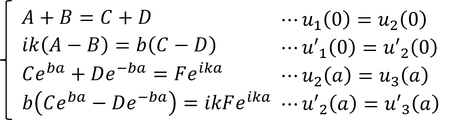
未知数5つに対して式が4つしかないので解くことはできないが、透過率Tを求めるためにはF/Aが分かればよいので、まず後半の2式を用いて
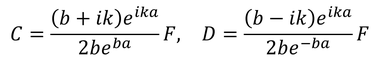
このようにC,DをFで表し、続いて前半の2式から得られた
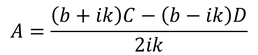
Aに、CとDを代入する。

ここから、A/Fが求められる。
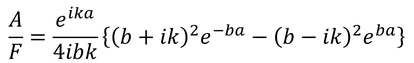
この逆数の2乗によって透過率Tが得られる。
ここで、ハイパボリックサイン(シンチ)sinhとハイパボリックコサイン(コッシュ)coshを用いてこれを簡単にする。

より、

となる。
これを2乗し、

ここで、

を用いて書き変える。

こうして、透過率

が得られる。
また、反射率をR=|B/A|^2と表すと、反射率と透過率の和が1になることから、
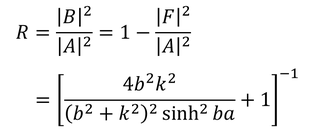
を得ることもできる。
トンネル効果
透過率の式に使われているbとkを元に戻し、エネルギーE,V_0で表す。

より、

ここでbaが非常に大きいとすると、sinh(ba)は

となるので、

と変形できる。+1も消去した。

せっかくなので、私たちが壁を通り抜ける確率を求めてみよう。ざっくり、eの部分だけに注目する。
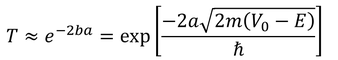
いま、50kgの人が10m/sの速さで、高さ10m,厚さ1mの壁に衝突することを考えると、ポテンシャルV_0と運動エネルギーEが
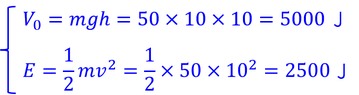
だから、透過率は

となる。0といってよいことが分かる。
