スピン
軌道角運動量Lとスピン角運動量Sには多くの共通点がある。すでに紹介している軌道角運動量Lの復習をしながら、スピン角運動量Sの性質について詳しく見ていこう。
昇降演算子
軌道角運動量には、3成分の交換関係がどれも0ではなく、それらが同時に決まらないという性質があった。

ところが、角運動量演算子の2乗と各成分の交換関係はどれも0で、それらは同時に決まる。

同様に、スピン角運動量も同じ性質があるとみてよいだろう。
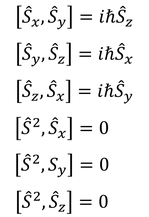
また、L^2とLzには共通の固有関数Y(θ,φ)があり、軌道量子数lおよび磁気量子数mを用いて、固有値方程式は次のように表される。

そこで、スピン角運動量Sについても同様に共通の固有ベクトルがあり、固有値方程式が次のように表されるとしよう。
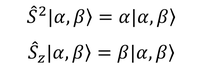
続いて、スピン角運動量演算子の特徴を詳しく見ていくために、次のような演算子を導入する。
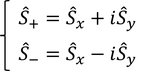
S+を上昇演算子、S-を下降演算子、まとめて昇降演算子と呼ぶ。上昇演算子と下降演算子の積は

であり、下降演算子と上昇演算子の積は
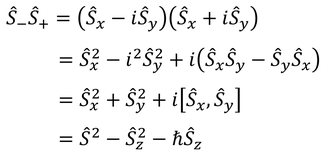
だから、上昇演算子と下降演算子の交換関係を計算すると、

となり、SzとS+の交換関係は
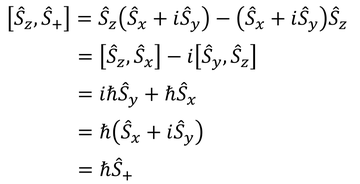
SzとS-の交換関係は
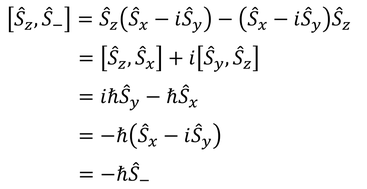
となる。さらに、S^2とS+の交換関係と
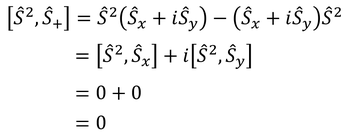
S^2とS-の交換関係

も求められる。
どうして昇降演算子と呼ぶのかというと、
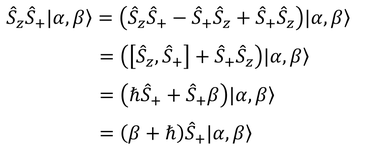
および
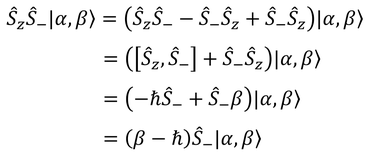
を計算することで、固有値βがhバーだけ上昇したり下降したりするからである。ただし、
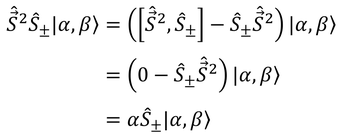
このように固有値αは変化しない。
スピン量子数
ところで、
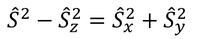
の固有値は正でなければならないから、固有値αとβの間には
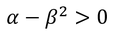
の関係があることが分かる。すなわち、αがある値のとき、βには上限と下限があるということである。
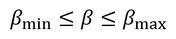
ここで、上昇演算子は固有値βをhバーだけ上昇させる作用があったから、
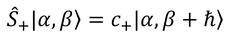
のようになるが、βが最大の状態に上昇演算子を作用させても上昇しないので、
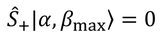
となるはずである。これに下降演算子を作用させると

こうして固有値αが求められる。同様に、下降演算子は固有値βをhバーだけ下降させる作用があったから、

となるが、βが最小の状態に下降演算子を作用させても下降しないので、
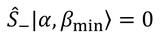
となるはずである。これに上昇演算子を作用させると
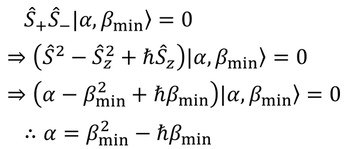
こうして固有値αが求められる。2通りの方法でαが求められたから、これらを比較することで
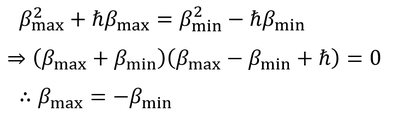
固有値βの最大値と最小値の関係が得られる。
ところで、固有値βが最小の状態に、上昇演算子をn回作用させることで最大の状態に達すると考えると、
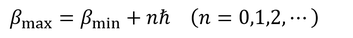
となるが、最大値と最小値の関係より

を得る。n/2は0,1/2,1,…の値を取る。n/2をさらにs表すことにすれば、
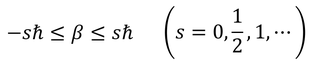
のように固有値βの範囲が定まる。sをスピン量子数と呼ぶ。スピン量子数sを用いると、固有値αは
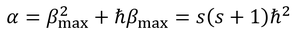
となる。さらに、固有値βを

と表すとき、mをスピン磁気量子数と呼ぶ。こうして、sやmによって状態が決定されるので、2種類の固有値方程式は

と表すことができる。
電子のスピン
スピン量子数は、電子のようなフェルミ粒子で1/2,グルーオンやウィークボソンなどのようなボース粒子では1であることが知られている。ここでは電子を考え、演算子や固有ベクトルの形を調べていこう。
スピン量子数がs=1/2のとき、スピン磁気量子数はm=-1/2, 1/2の2通り存在する。この固有ベクトルを、それぞれ

のように表そう。そして、スピン角運動量演算子を行列で表したときの成分を
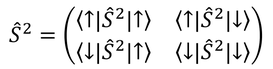
と表す。各成分を計算すると

となるから、

を得る。
同様に、z成分
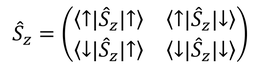
も求める。各成分を計算すると

だから、
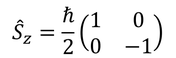
が得られる。
次は、これらに共通の固有ベクトルを求めよう。
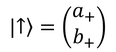
とおくと、Szの固有値方程式は
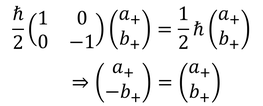
となるので、これを満たす

が得られる。あとは規格化して
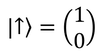
1つめの固有ベクトルが定まる。また、
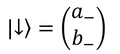
とおくと、Szの固有値方程式は

となるので、これを満たす

が得られる。あとは規格化して
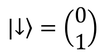
2つめの固有ベクトルが定まる。
さらに、昇降演算子を利用することで、次のようにSxやSyの行列を求めることもできる。

いま、状態ベクトルに上昇演算子を作用させた式

を考えて、これにエルミート共役なベクトル
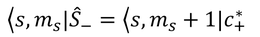
を掛けることで、
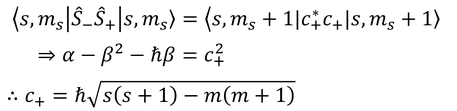
定数部分が得られる。これで、

より、上昇演算子の行列表示

が得られた。
同様に、状態ベクトルに下降演算子を作用させた式

にエルミート共役なベクトルを掛けることで
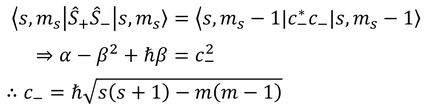
こうして定数部分が得られる。これで、

より、下降演算子の行列表示

が得られた。これで、スピン角運動量演算子の各成分の行列表示
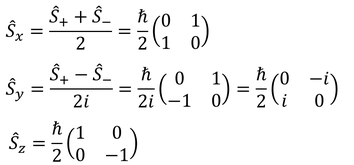
が得られた。ここで、

とおくと、
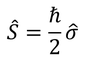
とまとめることができる。σをパウリ行列と呼ぶ。
