シュレーディンガー方程式
前章までで、電磁波には粒子的な性質があり、電子などの粒子には波動的な性質があることが分かってもらえたと思う。今回は、この物質波の振る舞いの定式化に挑戦しよう。
波動方程式

波の性質を記述する方程式を「波動方程式」という。例えば電磁波は電場Eや磁場Bの振動であり、

と表される。一般的に、波動方程式を満たすEやBを「波動関数」という。例えば、電場Eは


だから、

となる。これを元の波動方程式と比較し、

と置くことで一致する。ゆえに、波動関数Eが正しいことが分かった。ところで、前回角振動数ωと波数kの関係は「分散関係」と呼んだ。この関係が電磁波に関する分散関係というわけだ。
物質波に関する分散関係は、

であった。これを使って、物質波の波動方程式を求めてみよう。とりあえず波動関数を

とおき、分散関係を満たす波動方程式を目指す。電磁波と同様に波動関数をtやxで偏微分して、

ωとk^2を作り、分散関係の式へ代入すると、

となる。これでOK…と思いたいところだが、両辺を見比べてみると、右辺はsin関数, 左辺はcos関数になっており、両辺は一致しない。つまり、元の波動関数が誤りであることを表しているわけだ。困った……。
シュレーディンガー方程式
ではどうするか。困ったときは、ネイピア数eおよび複素数の力を借りる。例えば波動関数を、

とおくのだ。先ほどと同様に、この式をtやxで偏微分して、

ωとk^2を作り、分散関係の式へ代入する。すると、

という関係を導くことができる。これが物質波の波動方程式である。そして、両辺をhバー倍した、
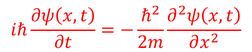
この式を「シュレーディンガー方程式」という。
演算子
なぜhバー倍したかを実感してもらうために、仮定した波動関数ψ(x,t)を使って左辺を計算してみよう。

ℎνは、エネルギー「E=hν」である。

つまり、こうすることでエネルギーの次元にして考えやすくするためだったわけだ。
ちなみに、波動関数ψ(x,t)のxによる偏微分を用いた、

という計算によって、運動量「p=ℎ/λ」を取り出すことができる。

いま導いた2種類の関係式から、エネルギーEと運動量pが、

これらの演算に対応していることが分かる。それぞれ「エネルギー演算子」「運動量演算子」と呼び、演算子であることを強調して、E、pの上に^を付けて表す。
ところで、自由粒子(位置エネルギー0)のエネルギーEは、運動量pを用いて

と表すことができるので、Eとpを演算子の形で表せば、

のように、(自由粒子の)1次元シュレーディンガー方程式を導くことができる。
これと同じ操作から、位置エネルギーV(x)を持っている場合の粒子のシュレーディンガー方程式を導くことができる。このとき、粒子のエネルギーEは

だから、このEとpを演算子で表すことで、

一般的な、「1次元のシュレーディンガー方程式」を導くことができる。
変数分離

定常波の波動関数は、xの部分とtの部分の積で表すことができる。原子に含まれる電子などは定常波になっているようなので、基本的にはそのような場合を考えることが多そうだ。そこで、波動関数ψ(x,t)が

と表せるときを考えよう。すると、シュレーディンガー方程式は

となる。ここで両辺をψ(x,t)=u(x)f(t)で割ると、

となり、左辺にt、右辺にxを固めることができる。tとxはそれぞれ独立に変化することができるが、両辺が常に等しくなるためには、一定の値であると考えるしかない。これを定数Eとおく。すると、

という2式(tの式、xの式)を作ることができる。このような操作を「変数分離」と呼ぶ。tの式は簡単に解くことができて、

となる(定数C)。このことから、波動関数ψ(x,t)が、

のように表せることが分かる。
続いてxの式に注目しよう。

この式は、「時間に依存しないシュレーディンガー方程式」と呼ばれている。今後は、位置エネルギー(ポテンシャル)V(x)の形を考えながら、この式を解くことが目的となる。
また、この式は( )の中身を

と置いて、

と表すこともある。Hを「ハミルトニアン」と呼ぶ。
