連続体の変形~ナビエの方程式~
応力テンソルとひずみテンソル

i軸に垂直な面にはたらくj方向の応力をτ_ijと書くことにしよう。9つの成分をまとめたテンソルを応力テンソルと呼ぶ。
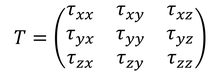
9つの成分があるが、力のモーメントのつり合いの関係から、添え字を入れ替えたτ_ijとτ_jiは等しいので、独立な成分は6つである。
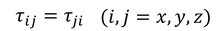
このようなテンソルを対称テンソルと呼ぶ。
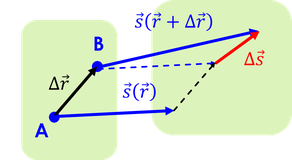
続いて、連続体の変形を表すことを考えよう。Δrだけ離れた2点がそれぞれ変位したときの相対変位をΔsとする。Δsが微小であるとき、
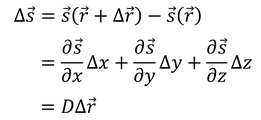
と近似できる。相対変位ベクトルΔsと相対位置ベクトルΔrをつなぐテンソルDを、相対変位テンソルまたは変形テンソルと呼ぶ。
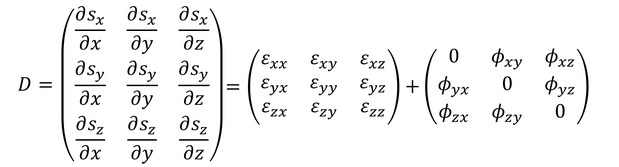
ここで、相対変位テンソルを、対称テンソルε_ijと反対称テンソルΦ_ijの和で表すことを考える。

これらのテンソルの成分を相対変位sを用いて表すと、

である。テンソルε_ijとΦ_ijがどのような変形を表しているのかを考えるために、z方向の変形が0(Δz=0)で、かつz軸に沿って変位が変化しない(Δs_x=0)であるとすると、相対変位テンソルΔsの成分は、
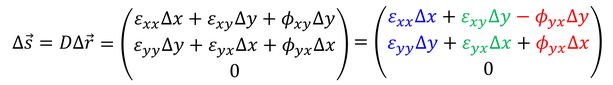
と書ける。

第1項は軸方向の伸縮を、第2項はひずみ変形を、第3項は回転を表していることがわかる。連続体の変形がこの3種類の変形に分類できることを、ヘルムホルツの基本定理と呼ぶ。また、ε_ijがひずみ変形を表していることから、ε_ijはひずみテンソルと呼ばれる。

次は体積ひずみに注目しよう。微小体積ΔxΔyΔzの直方体が、軸方向にそれぞれΔs_x,Δs_y,Δs_zずつ膨らんだとする。このとき、体積ひずみは、
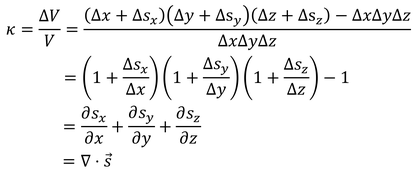
と計算できる。また、ひずみテンソルの対角成分ε_iiが、

であることから、体積ひずみはε_iiの和でも表され、
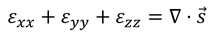
という関係が成り立つ。
弾性テンソル
応力テンソルτ_ijはひずみテンソルε_ijに比例する。
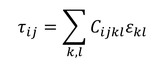
これを、一般化されたフックの法則と呼ぶ。以前紹介した「f=Eε」をさらに一般化した式である。ここで、C_ijklは弾性テンソルと呼ばれ、座標に寄らない等方テンソルの場合、

と表される。δ_ijはクロネッカーのデルタである。これを使って応力テンソルτ_ijを計算していくと、
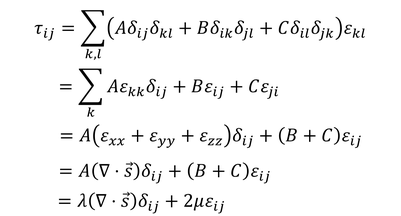
となる。新しい定数λとμを、ラメ定数と呼ぶ。
例えば、微小な体積部分が3方向から同じ大きさの圧力を受けているとき、その圧力は、
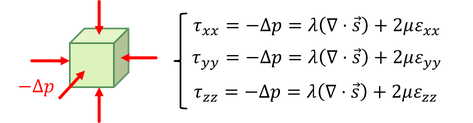
と表せる。すべて同じ大きさなので、3つの式を足して、
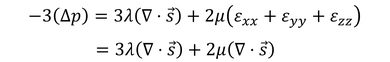
3で割ると、
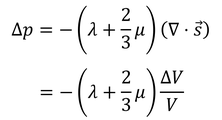
が得られる。ここで、
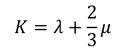
は体積変化の起こりにくさを表していて、体積弾性率と呼ばれる。
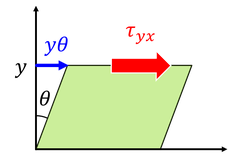
また、ひずみε_yxが
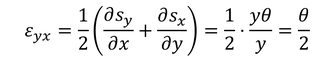
と表せるとき、せん断応力τ_yxは、

と計算できる。μはずれ変形の起こりにくさを表していて、剛性率と呼ばれている。
弾性体の運動方程式

微小領域に注目して、弾性体の運動方程式のx成分を考えてみよう。x方向の応力テンソルをまとめた

を使うと、
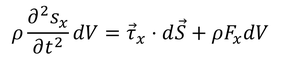
と表せる。F_xは単位質量当たりの力のx成分である。これを弾性体全体で足し合わせることで、弾性体全体の運動方程式になる。

2行目はガウスの発散定理を使って面積分を体積積分に変換した。積分記号を外すと、

となる。応力ベクトルの発散∇・τ_xは、

だから、運動方程式は、
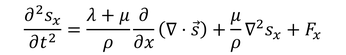
と変形される。同様にy,z方向についても考えてまとめると、
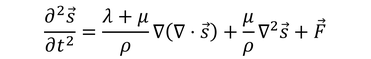
とすることもできる。これをナビエの方程式と呼ぶ。
流体の方程式
ここまでの話を流体に適用してみよう。流体の場合は、変形速度ベクトルΔvが相対位置ベクトルΔrによって記述できるとして、
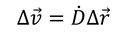
と表せるとする。2つのベクトルをつなぐテンソルは変形速度テンソルと呼ばれる。
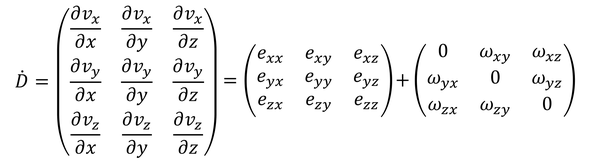
また、変形速度テンソルを対称テンソルと反対称テンソルに分けたとき、対称テンソルe_ijをひずみ速度テンソルと呼ぶ。それから、粘性による応力τ_ijがひずみ速度テンソルe_ijに比例するような流体をニュートン流体という。
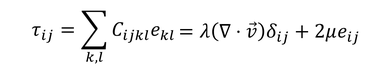
流体の運動方程式は、まず微小領域に注目して、

と立てる。ここで、左辺のDv/Dtは流体の移流加速度を表す実質微分
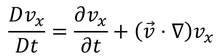
であり、pは静水圧、τは粘性応力である。
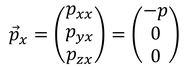
これを積分して流体全体の運動方程式にすると、
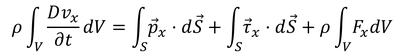
となり、右辺第1項と第2項にガウスの発散定理を適用して積分記号を外すと、
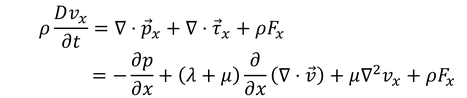
になる。y,z成分についても考えてまとめると、

となる。これをナビエ・ストークス方程式という。
体積が変化しない非圧縮性流体の場合は、速度ベクトルの発散が0になるから、

になり、非圧縮性かつ粘性のない完全流体の場合は、右辺第2項(粘性項)がさらに0になるから、

となる。また、非圧縮性かつ非常にゆっくりしたストークス流れの場合は、移流項(v・∇)vが0と見なせるから、
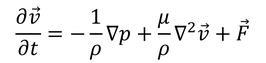
となる。
