ラグランジュ方程式
運動方程式は直交座標を使うととても簡潔にまとまるが、極座標を使って表すと複雑な形になってしまうことを前回確認した。もしも、直交座標であろうが極座標であろうが、同じ形で表されるような新しい”運動方程式”があれば、とても便利そうに思える。そこで登場するのがラグランジュ方程式だ。
1次元のラグランジュ方程式
x軸上を運動する物体の運動方程式は

と表される。また、運動量p

を使って、

と表すこともできる。
ここで、運動エネルギーT
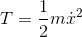
を速度vで微分すると、
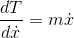
だから、
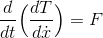
という式を作ることができる。
また、物体にはたらく力Fを保存力に限れば、Fは位置エネルギーUを使って

と表せるから、上の式は
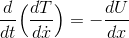
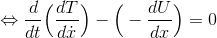
になる。ここで、
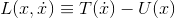
とおくと、

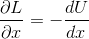
だから、

になる。この式を「ラグランジュの運動方程式」または「ラグランジュ方程式」と呼ぶ。また、Lをラグランジアンという。
2次元のラグランジュ方程式
続いて、平面上を運動する物体を考える。ニュートンの運動方程式は、

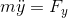
と表される。ここで、運動エネルギーT

を速度の成分vx,vyで微分すると、それぞれ
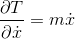

だから、運動方程式は、

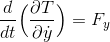
と変形される。
ここで、力Fを保存力に限れば、Fの成分Fx,Fyは位置エネルギーUを使って
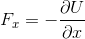

と表されるから、運動方程式は、
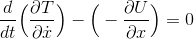
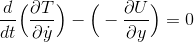
になる。
ここで、ラグランジアンLを
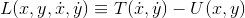
とすると、

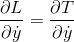


だから、

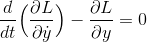
このように、ラグランジュ方程式を導くことが出来る。
極座標を使ったラグランジュ方程式
ここまではごく自然な流れだと思う。それでは、極座標を使ったラグランジュ方程式を考えてみよう。まず、ニュートンの運動方程式は


であった。
また、r方向、θ方向の速度を使えば、運動エネルギーTが

となるから、これを速度のr成分、θ成分で微分すると、それぞれ

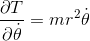
になる。ここで、これらの式をそれぞれ時間tで微分すると、


になる。これで、運動方程式は
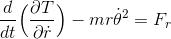

という形になる。さらに、Tはrの関数でもあるから、これをrで微分すると、

になるので、運動方程式のr方向の式は、
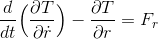
と書ける。
ここで、力Fを保存力に限れば、Fと位置エネルギーUの関係は、

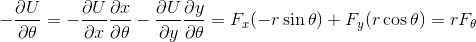
と表せるから、運動方程式は

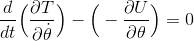
になる。
ここで、ラグランジアンLを

とすると、
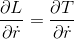

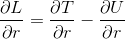

だから、
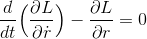
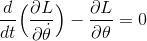
このように、ラグランジュ方程式を作ることが出来る。直交座標によるものと式の形を比較してみよう。まったく同じだということに気づくだろう。このことが大切なのだ。
