等確率の原理
前回は速度空間を考えることで分子の微視的状態を数えたが、今回は位置も考慮に入れることにしよう。
量子力学的微視的状態数
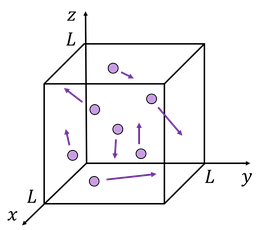
一辺Lの立方体にN個の分子が存在している。このとき、分子が取り得る微視的状態数を、前回の速度に加えて位置も考慮して考えてみよう。分子は非常に小さいので、量子力学のときにも登場した式を使えばよさそうだ。
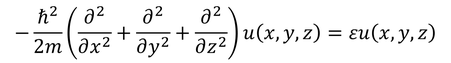
これを、時間に依存しないシュレーディンガー方程式という。ポテンシャルのない自由粒子を考えている。波動関数u(x,y,z)がそれぞれの成分に分離できるとすると、
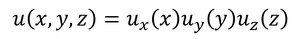
シュレーディンガー方程式も3成分に分離できる。
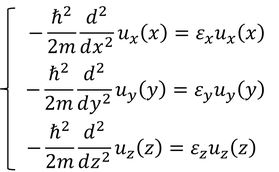
とりあえずx成分の式を解くことにする。この式を、
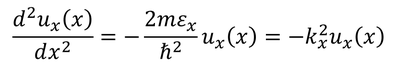
と書き変えることで、一般解
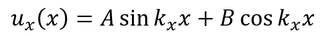
を得る。また、波数kを用いたエネルギー固有値

も得られる。

ここで、境界条件を導入しよう。箱の両端で存在確率が0になるように、x=0,Lにおける波動関数を0とする。
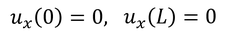
これらより、
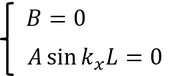
となり、波数kは、整数nを用いて

でなければならないことが分かる。y,z成分についても同様に
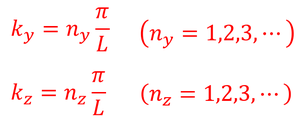
となる。
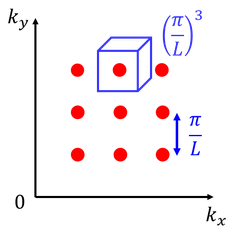
つまり、波数kはとびとびの値を取るということだ。さらに、波数空間上の体積(2π/L)^3ごとに1つの状態を表していることがわかる。

では、k~k+dkの範囲にあたる微視的状態数を求めてみよう。そのためには、波数空間上の球殻の体積4πk^2dkを(π/L)^3で割ればよい。ただし、kの成分はどれも正の値しか取らないので、8で割らなくてはならない。
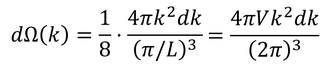
ただ、波数ごとの状態数は考えにくいので、kをエネルギーεに直そう。kをεで表すと

であり、これをεで微分することで、

dεを得ることもできる。これで、
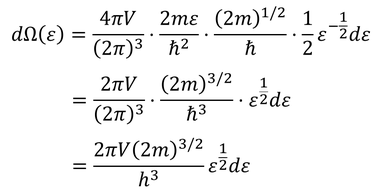
微視的状態数dΩをεを用いて書き直すことができた。
あとは、この式を0~εの範囲で積分すると、ε以下のエネルギーを持つ微視的状態数を求めることができる。
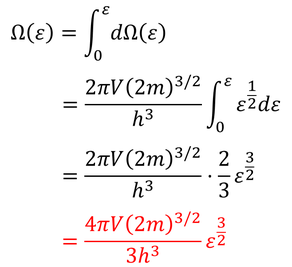
位相空間

位置と運動量の空間のことを「位相空間」または「相空間」と呼ぶ。位相空間上の1点により、分子の運動は記述される。ここではエネルギー0~εを持つ粒子が取ることができる位相空間の体積を求めてみよう。位相空間上の微小体積を積分すればよい。
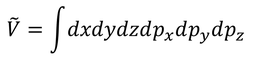
ただし、分子は体積Vの容器に閉じ込められているわけだから、

とすれば、
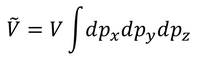
となる。残りの積分は、運動空間における体積である。

運動量空間上で、球殻の体積4πp^2dpを積分することを考えよう。
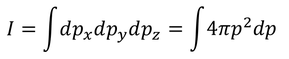
ただし、エネルギー0~εを持つ分子を考えたいから、運動量pをエネルギーεで表しておく。

pをεで微分する。
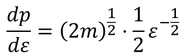
これらより、運動量空間上の体積Iは、
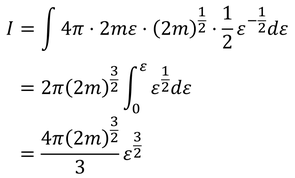
となるから、位相空間上の体積が、

こうして求められる。
微視的状態数Ω(ε)とこの体積とを比較すると、
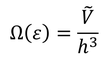
という関係があることが分かる。
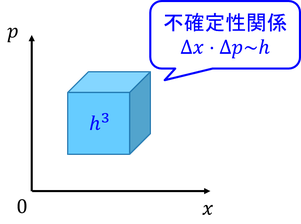
量子力学によると、位置xと運動量pの値には、プランク定数hと同程度のあいまいさを持つという。これを不確定性関係と呼ぶ。y成分,z成分についても同じことがいえるから、位相空間上で分子は体積h^3に1つずつ状態を持っていると言える。
3N次元球の体積
気体の分子がN個の場合、全体の微視的状態数はどのように考えたらよいだろう。さっき求めた、分子1個における微視的状態数と位相空間の体積との関係
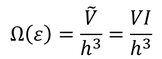
これを使って考えてみる。
まず、分子が1個のときh^3で割る必要があるのだから、分子がN子であればh^(3N)で割らなければならない。
続いて、粒子が1つの場合

だったから、N個の場合は
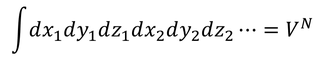
となる。
最後に運動量空間上の体積Iは、分子が1個のときは
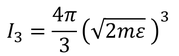
となり、これは、半径√(2mε)の球の体積と見ることができる。だから、分子がN個のときは、エネルギー全体をEとして、半径√(2mE)の3N次元球の体積を考えればよいことが分かる。まとめると、N個の分子の微視的状態数は、

と表せる。
半径1のn次元球の体積Cnは、

である。分母はガンマ関数と呼ばれるもので、定義は
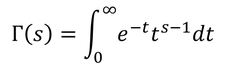
である。この式は、mが1以上の整数のとき、
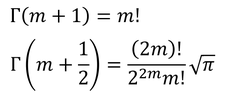
と書き変えられる。
このことから、半径rのn次元球の体積は、
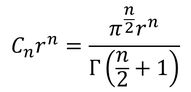
であり、半径√(2mE)の3N次元球の体積は、
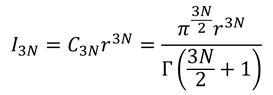
であることが分かる。
これで、N個の分子の微視的状態数

が得られた。
