マクスウェルの速度分布
気体の分子は空気中を飛び回っている。では、その速さはどのくらいなのだろう。いくつかの方法で求めてみよう。
二乗平均速度
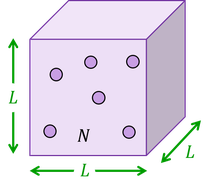
一辺Lの立方体の容器内に、質量mの分子がN個入っている。1個の分子が1枚の内壁Sへ速度vで衝突したとする。Sに垂直な速度の成分をv_xとすると、

だけの力積をSから受け取る。また、同じ分子が1往復してSに再衝突するまでの時間が
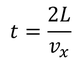
だから、1秒間にSに衝突する回数は
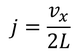
となる。以上より、1個の分子が1秒間あたりにSから受け取る力積
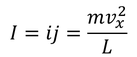
が得られる。また、1秒間あたりの力積を「平均の力」という。
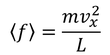
1秒間あたりに、分子はこの力をSから受け取り、また与えているとうことになる。N個の分子全体がSへ与えている力は、
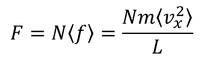
である。ここで、対称性から
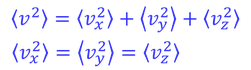
この2つの仮定を行うと、
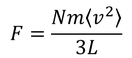
となる。この力を面積L^2で割ることで、
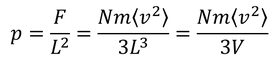
気体の圧力を得る。圧力は気体の状態方程式によって
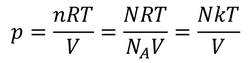
とも表されるから、2式を比較することにより、
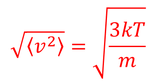
を得る。これを「二乗平均速度」という。ルートを取っていることから「根二乗平均速度」や「二乗平均平方根速度」とも呼ばれる。

驚くほど速いと感じるのではないだろうか。
二乗平均速度を用いて、気体の内部エネルギーを求めることもできる。運動エネルギーの平均をN倍することで、
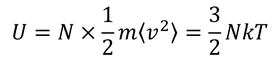
を得る。あとで使うので覚えておこう。
マクスウェルの速度分布
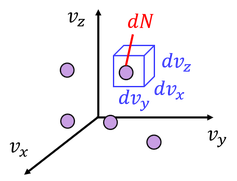
では、どのくらいの速さの分子が、どのくらい存在しているのだろうか。分布を求めてみよう。そのため、各分子の速度の成分を軸に取ったグラフを考える。これを「速度空間」と呼ぶ。速度空間上の1点が、1つの分子の速度を表している。
速度空間上の体積dvxdvydvzの内部に、dN個の分子が含まれているとする。全体Nとの割合を
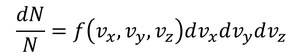
と表そう。存在確率なので、速度空間全体で足し合わせると1になる。
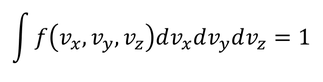
関数f(vx,vy,vz)はどのような形なのだろう。ひとまず、速度の各成分vx,vy,vzは独立かつ対称的だから、それらは分離でき、同じ形の関数gで表せるのではないだろうか。
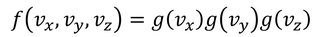
また、各成分は、正の向きの分布と負の向きの分布に対称性があると考えられるので、変数は2乗の形になっていると推測される。


もう少し詳しく考えてみよう。vxに注目するため、vy^2やvz^2を定数cとして、このときのg(c)=nとすると、
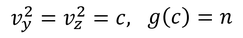
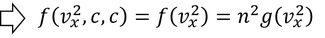
という式が得られる。vyやvzについても同様に考えると
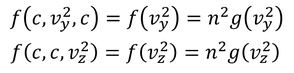
となるから、これらより
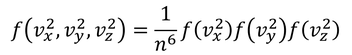
関数fが持つ関係式が分かる。関数fを3つ掛けた結果、同じ形の関数fになるということだ。この関係を満たす関数として、定数C,αを用いて
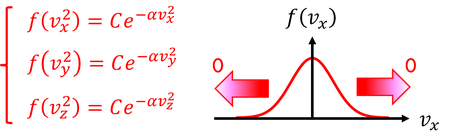
を考えることができる。eの指数が+の場合も上の関係は成り立つが、速度の成分が+∞や-∞のときに確率が0になって欲しいので、eの指数は-になると予想できる。
これらを用いると、f(vx,vy,vz)は
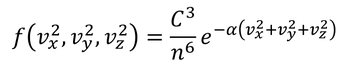
となる。定数部分をAとおき、速度vを用いると

となる。
マクスウェルの速度分布
では、定数Aとαを決定して、関数f(v^2)を求めよう。まずは確率を速度空間上で足し合わせると1になるという関係を使う。
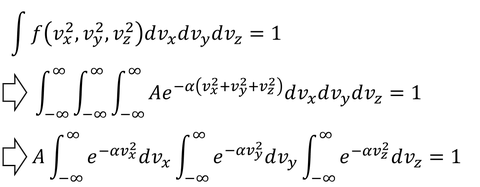
ここで、ガウス積分の公式
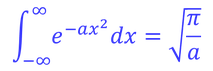
を用いると、
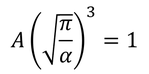
となる。ここから、
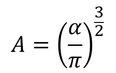
定数Aをαで表すことができる。すると、f(v^2)は
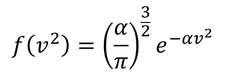
となる。
続いて定数αを決定するために、気体の内部エネルギーを考えてみよう。気体の内部エネルギーは、気体分子の運動エネルギーの平均をN倍することで求められる。
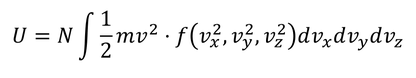

速度の成分による積分を、速さによる積分に変換しよう。速度空間上で半径v,厚さdvの球殻を考えると、その体積は4πv^2dvになるから、球殻に含まれる分子の存在確率は
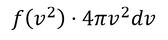
と表される。これを利用して、気体の内部エネルギーを求める。
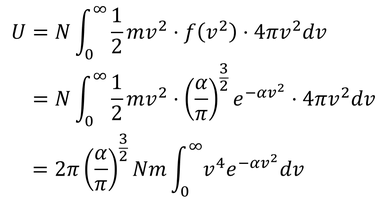
ここで、積分公式
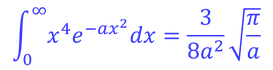
より、
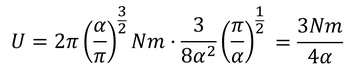
となる。この結果を先に求めていた気体の内部エネルギー
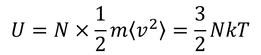
と比較することで、
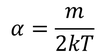
αが求められる。これで、関数f(v^2)が得られる。

これを、「マクスウェルの速度分布」という。
平均の速さ
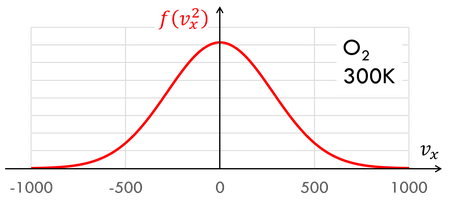
速度のx成分と、その存在確率(確率密度f(v^2))をグラフにすると上のようになる。速さと存在確率の関係は、内部エネルギーを求める途中で導出した
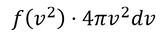
を考えればよい。
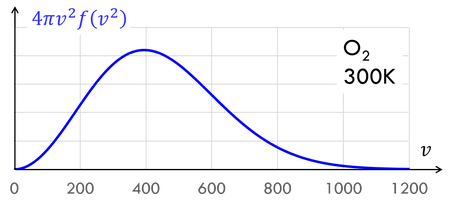
速さと存在確率をグラフにするとこのようになる。300Kにおける酸素分子の二乗平均速度は483m/sだったが、速さのピークは約390m/sになっていることが分かる。
では、「平均の速さ」はいくらだろうか。計算してみよう。
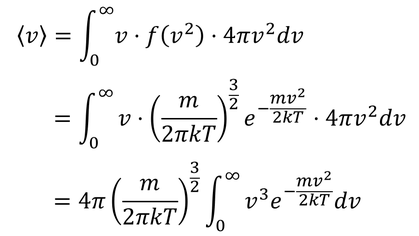
ここで、積分公式
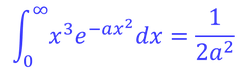
を利用すると、
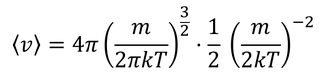
となるから、平均の速さ
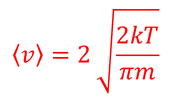
が得られる。

比較をすると、二乗平均速度よりもわずかに小さな値になっていることが分かる。
最後に、f(v^2)を利用して二乗平均速度を求めておこう。
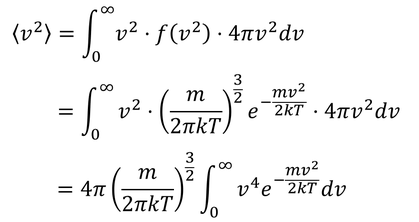
積分公式
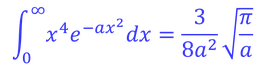
を用いることにより
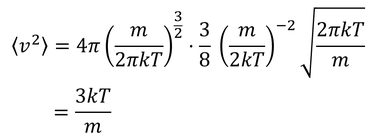
よって、
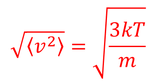
二乗平均速度が得られる。
