重力場の方程式
一般相対性理論には基礎となる方程式が2種類ある。ひとつめの測地線方程式は、曲がった時空内を物体がどのような経路をたどるかを表す方程式で、いわゆる一般相対性理論における運動方程式である。ふたつめは時空の曲がり具合と時空を曲げる原因を表す方程式で、「アインシュタイン方程式」と呼ばれる。
リーマン曲率テンソル
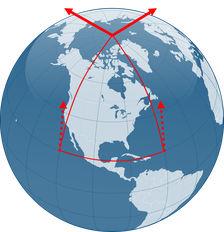
空間が曲がっていると、平行なベクトルを同じ点に移動させると平行でなくなる。平面であれば一致するはずである。だから、ある位置に置いたベクトルを、2通りの経路に沿って移動させたとき、移動後のベクトルの差を調べることで、時空が平坦か曲がっているかを判断できるのだ。
まず、位置x→x+dx→x+dx+δxとベクトルVを平行移動させていく。x+dxでのベクトルは、

と表すことができ、続いてx+dx+δxでのベクトルは、
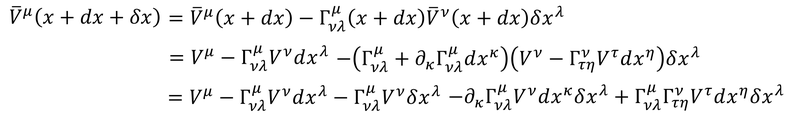
となる。2行目ではクリストッフェル記号をテイラー展開している。
次は経路を変えて、x→x+δx→x+δx+dxと移動させたベクトルは、今の結果のdxとδxを入れ替えることで得られるので、

である。これらの差を計算すると、
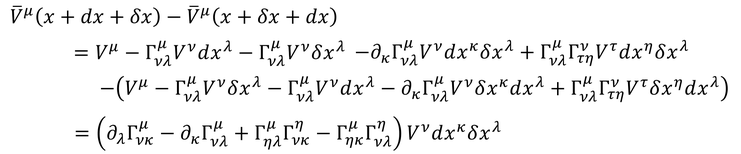
となる。カッコの中身

が時空の曲がりを表していて、これを「リーマン曲率テンソル」と呼ぶ。平坦な時空であれば0になる。
リーマン曲率テンソルには4つの添え字μ,ν,λ,κがあり、それぞれ0~3の値を取るので、合わせて4^4=256成分もあることになる。ただし、

という関係や、
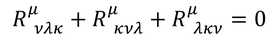
という関係があるため、独立な成分は95成分まで減らすことができる。
さらに、この式に計量を掛けると、
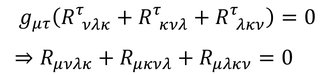
添え字を下げることができる。リーマン曲率テンソルの定義から、第1項は、
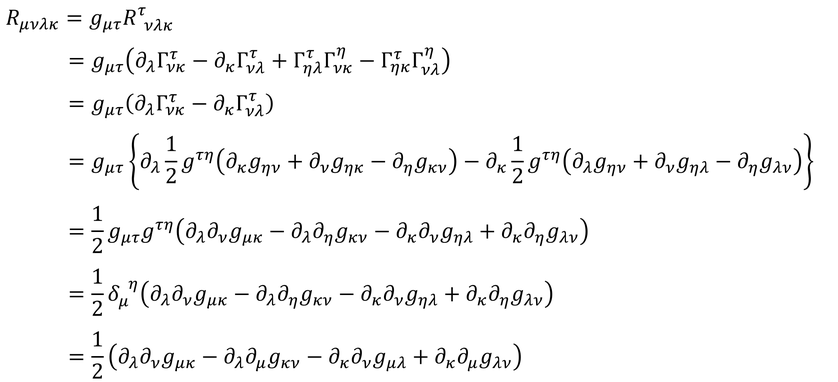
となる。ただし、局所的慣性系を考えることで、計量の微分は0とした。この式より、

の関係が得られるため、リーマン曲率テンソルの独立な成分が20個であることが分かる。一応書き出しておくと、上側の3つの関係式から

の21成分が得られ、下側の関係式によって1成分減って、20成分になる。
アインシュタインテンソル
リーマン曲率テンソルの共偏微分を計算しよう。局所慣性系を考えるとクリストッフェル記号は0だから、普通の微分と見なすことができる。

この結果から、

という関係を得る。これを「ビアンキの恒等式」と呼ぶ。 特に、ν=μのとき、

となるが、ここで

を「リッチテンソル」と呼び、リッチテンソルを使うと、ビアンキの恒等式は、
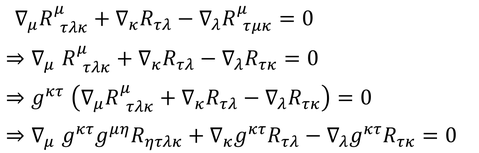
となる。さらに、

を「スカラー曲率」と呼び、これを使うと、

となる。ここで、カッコの中身

を「アインシュタインテンソル」と呼び、時空の曲がり具合を表している。アインシュタインテンソルは、

の関係を満たす。
エネルギー運動量テンソル

時空が曲がる原因は重力であり、重力は質量を持つ物体の周りに生じる。特殊相対性理論から、質量はエネルギーと等価であるから、重力の原因はエネルギーということもできる。ここでは質量やエネルギーが連続的に分布した運動量を持つ流体と見なすことで、時空が曲がる原因を「エネルギー運動量テンソル」によって表すことにしよう。エネルギー運動量テンソルT^μνは、x^νの面を通過する4元運動量p^μの流れである。流れは、粒子の数密度nと4元速度uの積で表す。
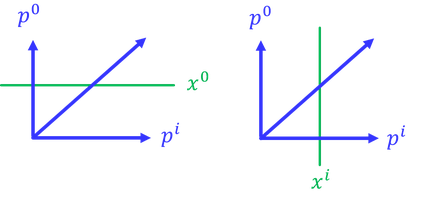
では、エネルギー運動量テンソルの成分を求めていこう。流体の速度がゆっくりになるような局所慣性系を選択すると、4元速度の0成分は光速c,1~3成分は3次元速度v^iと見なせる。まず、00成分は、運動量p^0=mu^0の流れnu^0だから、
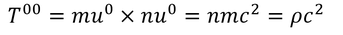
である。これは、「エネルギー密度」を表している。
i0成分は、運動量p^i=mu^iの流れnu^0だから、
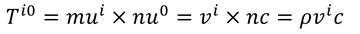
である。これは、「運動量密度」に光速cを掛けた量になっている。
0i成分は、運動量p^0=mu^0の流れnu^iだから、
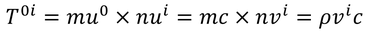
である。これは、「エネルギー流束」を光速cで割った量になっている。i0成分と同じ結果だが、運動量の0成分はエネルギーだから、エネルギーを主語にした言い方にしている。

ij成分も計算すると、
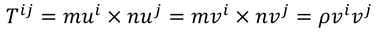
となる。これは、i=jのときは「圧力」を表し、i≠jのときは「応力」を表す。
エネルギーを運動量テンソルの成分をまとめると、

である。ここで、流体全体の速度が0になるような流体静止系を選び、流体を粘性のない完全流体とする。このテンソルは対角成分を残して0になる。圧力の成分はミクロな粒子の速度の2乗の和なので0にならない。また、パスカルの原理から圧力の成分はすべて等しい。

これでも十分見通しがよいが、ここではさらに圧力0の流体を考えよう。すると、

となり、この成分は、

と表すことができるので、これと比較して、圧力がpの流体のエネルギー運動量テンソルの成分が

と表されることが分かる。これは局所慣性系であるが、一般の座標系では

となる。
アインシュタイン方程式
時空の曲がり具合はアインシュタインテンソルで表され、時空が曲がる原因はエネルギー運動量テンソルで表されるのであった。これらは定数κを用いて
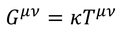
と結ぶことができる。この式が、一般相対性理論において重力場の方程式を表す「アインシュタイン方程式」である。アインシュタイン方程式は重力が強い場合にも成り立つ式だが、弱いときにはニュートン力学を満たす必要がある。これを踏まえて定数κを求めよう。
ニュートン力学には、ポテンシャルと質量分布の関係を表す式に「ポアソン方程式」がある。

確かめておく。ポアソン方程式へ、重力場gとポテンシャルΦの関係式
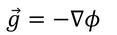
を代入すると、
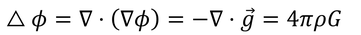
となる。全体を体積積分し、
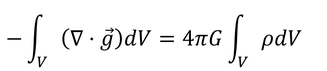
ガウスの発散定理によって左辺を面積積分に直し、右辺は質量をMとして書き直す。
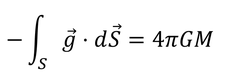
重力場のベクトルが、半径rの球面を貫いているとすれば、左辺は球の表面積を用いて書き直せるから、
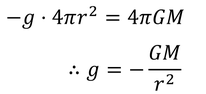
こうして重力場を求めることができる。すなわち、重力場gの中に質量mの物体を置いたとき、この物体が受ける力は

である。この式は、万有引力の法則を満たす。よって、ポアソン方程式をニュートン力学における重力場の方程式と見なしてよいことが確かめられた。
では、重力が非常に小さく、計量がミンコフスキー計量からのわずかなずれで表されるとしよう。

すると、この微分は
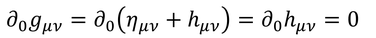
である。アインシュタイン方程式に計量を掛けて計算すると、
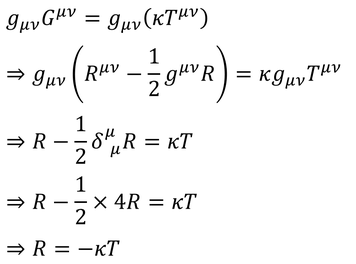
こうしてスカラー曲率が得られる。これを、もう一度アインシュタイン方程式に戻すと、
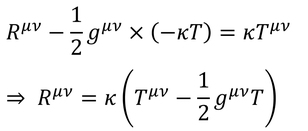
を得る。ニュートン力学では重力の原因は質量(エネルギー)だから、エネルギー運動量テンソルを思い出して、00成分のみを考えることにしよう。

この結果は、リッチテンソルの00成分と等しい。
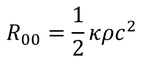
また、リッチテンソルはその定義から、
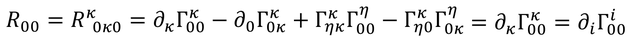
とも表される。クリストッフェル記号も定義に沿って計算すれば、

から、

であるから、リッチテンソルの00成分は、
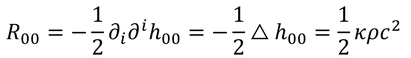
となる。あとは、h_00が分かればκが得られる。 h_00は、測地線方程式を用いて求めよう。測地線方程式は
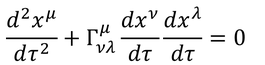
である。添え字を書き変えると
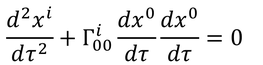
となり、さっき求めたクリストッフェル記号の式が使える。
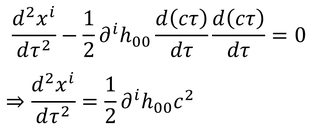
固有時τを時間tに直すと、ニュートンの運動方程式と比較できる。

これで、h_00が得られる。

これをリッチテンソルの00成分の式へ代入し、計算すると、
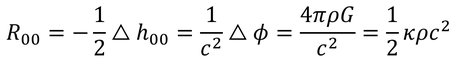
となるから、係数κが得られる。

これで、アインシュタイン方程式が導出できた。
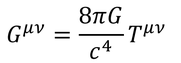

ここでアインシュタインは考えた。この式を宇宙全体に適用すると宇宙は重力で縮んでしまう。アインシュタインは宇宙は定常なものにするため、「宇宙項」と呼ばれる項Λgを加えた。
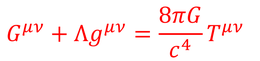
ただし、観測によって宇宙が膨張していることが分かると、定常でなければ宇宙項は必要なかったとアインシュタインは後悔したと言われている。しかし、最近のさらなる観測によって、宇宙の膨張は加速度的に進んでいることが分かり、宇宙項の必要性が見直されてきている。
