等価原理
特殊相対性理論では重力がうまく扱えない。また、特殊相対性理論で扱っている座標系は慣性系であるため、加速度系などの一般の座標系に適用することができない。重力や加速度系を考えることで、特殊相対性理論では見えてこなかった現象が見えてくる。
等価原理

重力は扱うのが難しい。では、打ち消してしまえばよいのではないか。例えば、屋根から飛び降りると、空中にいる間は重力を感じないはずだ。これは、重力とともに、上向きに「慣性力」と呼ばれる見かけの力がはたらいているからで、重力と慣性力がつり合っているため、自由落下中の人は重力を感じない。少し物騒なので、自由落下をしている窓のないエレベーターを考えよう。このエレベーターの中にいる人には景色が見えないから、宇宙空間に漂っているのか、それともエレベーターとともに自由落下しているのかを判断することは難しいだろう。また、宇宙空間でエレベーターを上向きに加速させた場合、人には加速度とは逆向きに慣性力がはたらき、重力と同じはたらきをする。窓がなければ、エレベーター内の人にとって、自分にはたらいている力は重力なのか慣性力なのか判断することはできない。すなわち、重力と慣性力は区別がつかないのだ。このことを、「等価原理」と呼ぶ。

地球上での重力加速度をgとすると、質量mの人にはたらく重力はmgである。また、加速度gで上向きに加速度運動をするエレベーター内の人には、加速度と逆向きに慣性力mgがはたらく。重力の大きさを表す比例定数としての質量を「重力質量」と呼び、物体の動かしにくさを表す「慣性質量」と呼ぶ。この2種類の質量は別々に定義されているものだが、等価原理により、区別ができないことがわかる。実際に、実験ではかなりの精度で一致することが分かっている。

気を付けなくてはならないのは、エレベーターが大きすぎてはいけないことだ。地球は球体で重力は地球の中心へ向かうので、エレベーター内の両端ではわずかに重力の向きは異なるだろう。また、地球の周辺では、地球の表面から離れるにしたがって重力は弱くなるため、エレベーター内の上下でわずかに重力の大きさが異なるはずだ。しかし、宇宙空間で一定の加速度を持って運動しているエレベーター内に生じる慣性力の向きや大きさはどこでも同じである。だから、本当はこうして重力と慣性力を区別することができるのだが、今後は非常に小さなエレベーターを考えることにして、重力と慣性力は全く区別できない場合があるとする。これを「局所慣性系」と呼ぶ。
時間の延び

では重力のはたらきを見ていこう。無限遠方から地表に向かって自由落下するエレベーターを考える。無限遠方では重力の影響はなく、エレベーター内の重力は慣性力が打ち消しているから、無限遠方の時間Δt∞とエレベーター内の時間Δtは等しいと考えてよい。
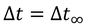
エレベーターが地表付近にやってきたときの地表に対する速さをvとすると、逆に、エレベーターに対して地球も速さvで運動していることになるから、地表の時間Δt0はエレベーター内の時間よりもゆっくり進む。

エレベーター内の時間よりも地表の時間がゆっくり進むということは、エレベーター内の時間と無限遠方の時間は等しいわけだから、重力の影響で時間がゆっくり進むようになったと考えることができる。
光の振動数の変化

時間が変化するということは、光の波長や振動数にも影響を及ぼす。地球から出た光は時間Δt0でN回振動しているとすると、この振動数ν0は

である。同様に、無限遠方での光の振動数を表すと、
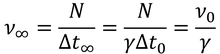
となり、振動数が小さくなっている(波長が大きくなっている)ことが分かる。すなわち、重力は光の振動数が大きくする(波長を小さくする)はたらきがあるということだ。
