相対性原理
1687年にアイザック・ニュートンは『自然哲学の数学的諸原理(プリンキピア)』で3種類の内容からなる運動の法則を発表した。第1法則は慣性の法則、第2法則は運動の法則、第3法則は作用反作用の法則である。
ガリレオの相対性原理
16世紀。コペルニクスが地動説を確信していたころ、地動説に反対する天動説の支持者たちは次のように主張した。
- 真上に投げ上げた小石は元の位置に戻ってくる。地球が移動しているのなら、小石は後ろへ飛んで行ってしまうはずだ。
この意見に対し、ガリレオ・ガリレイは次のように考えた。
- 一定の速さで動く船のマストから小石を落とすと、小石は真下へ落ちる。だから、小石が足元に落ちることは、地球が動いていないことの理由にはならない。

ガリレオはこの現象について、
- 物体には今の運動を保とうとする性質がある。だから小石は、船とともに等速で移動しながら落下する。そのため、船とともに移動する人にとって小石は真下に落下したように見えるのだ。
と考えた。慣性の法則である。ガリレオは、ニュートンが運動の3法則を発表するよりも前に、慣性の法則に気付いていたのだ。
小石の運動は、船上の人には自由落下に見える。しかし、船の外から見ると、小石は水平投射になっている。水平投射は水平成分が等速直線運動、鉛直成分が自由落下の運動だ。観測者の立場によって異なる運動ではあるが、力を受けていない水平方向の運動はニュートンの運動の第1法則(慣性の法則)に従っているし、重力を受けた鉛直方向の運動は第2法則に従っている。このような、ニュートンの運動の法則が成り立つような立場を「慣性系」と呼ぶ。
静止、または等速で運動している系を慣性系と呼ぶわけだが、静止という状態はどちらの観測者の立場で見るかによって異なる。このようなものの見方を「相対的」という。

ニュートンは、広い宇宙のどこかには「絶対静止系」があると考えた。今後は、絶対静止系に対して等速で動いている系のことを「慣性系」と呼ぶことにしよう。
先に見たように、異なる慣性系であってもニュートンの運動の法則が同様に成り立つ。これを「ガリレオの相対性原理」と呼ぶ。
ガリレイ変換
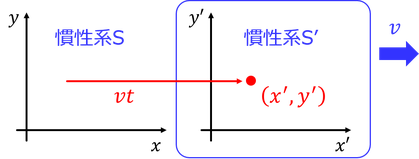
慣性系Sと、Sに対してx軸方向へ一定の速度vで運動する慣性系S’があるとする。2種類の座標がちょうど重なったときをt=0とすると、慣性系S'とともに運動する点(x',y')は、慣性系Sから見ると、時刻tにおいて

と表すことができる。この式は慣性系SとS'の変換を表しており、これを「ガリレイ変換」という。
運動方程式(ma=F)をガリレイ変換してみよう。加速度の成分を微分形式で表すと
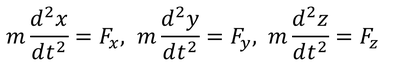
となる。ここでxの2階微分をガリレイ変換の式から計算すると、
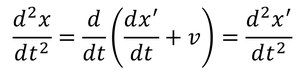
となるので、運動方程式は

となる。同様にy成分、z成分の加速度も求めると、運動方程式は
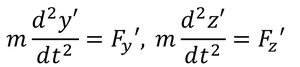
となる。元の運動方程式と同じ形になっていることが分かるだろう。つまり、
- ガリレイ変換によって、運動方程式の形は変わらない
ということ。ガリレオの相対性原理は、このように言い換えることができるのだ。
波動方程式のガリレイ変換

力学の基本式である運動方程式が、ガリレイ変換によって形を変えないことが分かった。では、他の式はどうだろう。例えば、一般的に波の特徴を表す波動方程式は次のような形で表される。
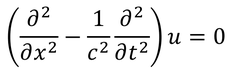
cは波の速さである。なお、簡単のためにx軸方向の波を考える。座標のガリレイ変換は、
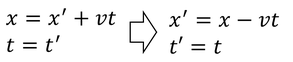
である。時間tは変わらない。
ガリレイ変換の式を利用してxによる偏微分を計算すると、
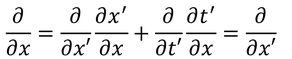
となるので、2階微分は

となる。続いてtによる偏微分を計算すると、
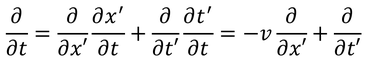
になるので、2階微分は

となる。
これで、波動方程式はガリレイ変換することで
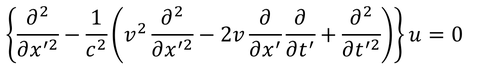
となる。明らかに元の形と異なっている。波動方程式はガリレイ変換によって形が変わるのだ。その原因は式の中に速さcが含まれているからで、cは媒質に対する波の速さである。そのため、媒質が静止しているように見える慣性系(媒質静止系)Sの場合にのみ、波動方程式は元の形で表されれるのだ。

速さcは媒質に対する速さである。媒質静止系における波の速さがcである。では、媒質を必要としない波の場合、cは何に対する速さなのだろう。例えば光は真空中を伝わる。光の速さは、何に対する速さなのだろうか。
