時間と空間

　特殊相対性原理と光速度不変の原理からアインシュタインは相対性理論を作り上げた。今回は、時間に関する常識を疑う所から始めてみよう。

同時性の不一致

　地上に対して速度ｖで移動する電車の中央から光を放射する。電車の中から光を見ると、

という時刻で同時に光が両端に到達することを観測する。

　では電車の外から見るとどうなるかというと、電車が動いていることを観測するわけだから、まず時刻

に光が後端に達し、その後、時刻

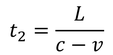
に光が前端に達することを観測する。同時ではない。このように、慣性系が違えば同時が同時でなくなってしまうのだ。その要因は光速度不変の原理にある。これまでは時間が誰から見ても同じであるという「絶対時間」という考え方が当たり前だった。ところがアインシュタインが光速度不変の原理に気が付いたことで、時間が絶対的なものではなく、相対的なものであることが分かったのだ。

時空図

　1次元方向に運動する物体の位置と時間を表すため、横軸に位置ｘを、縦軸に光速と時間の積ｃｔを取ったグラフを考えよう。これを「時空図」と呼ぶ。例えば、ずっと静止している物体の様子は、縦軸に沿った直線で表現できる。

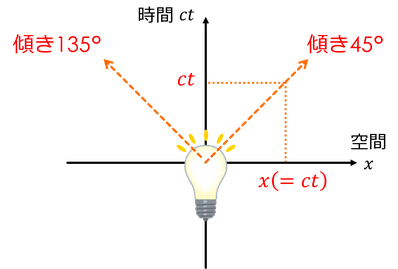
　時刻0，位置0で放射された光を時空図上に表すと、正の向きに進む光は傾き45°の直線に、負の向きに進む光は傾き135°の直線になる。どんなものも光の速さを超えられないため、光よりも遅い物体の運動は、傾きの大きさが45°よりも急な直線になる。

　時空図上で直線の傾きが45°よりも急な2点は移動が可能である。この関係を「時間的」という。一方、45°よりも傾きが緩やかな2点は行き来できない。この関係を「空間的」という。

　速度ｖで正の向きに移動する電車の様子を時空図上に表すと、傾きｃ/vの直線になる。原点を通るこの直線は、電車内の慣性系S'にとっての位置x'=0の点の集まりである。つまり、慣性系S'にとっての時空図の時間軸となっている。

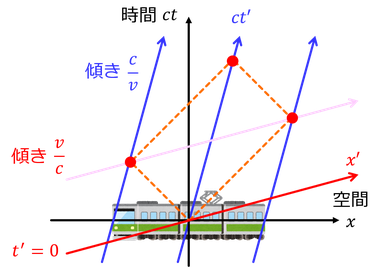
　電車の中央から光を放射した。この様子を地上の慣性系Sについての時空図上で見ると先に電車の後端に光が達し、そのあと前端に達している様子が分かる。その後、両端に鏡があるとして反射して返ってきた光は電車の中央で交わることになる。この時刻はどちらの慣性系においても同時である。

　ところで、光が両端に達した時刻は電車内の慣性系S'にとっては同時である。この2点を結んだ直線の傾きは、対称性からv/cとなることが分かる。この直線を原点に合わせると、慣性系S'にとっての時空図の空間軸が得られる。

時間の延び

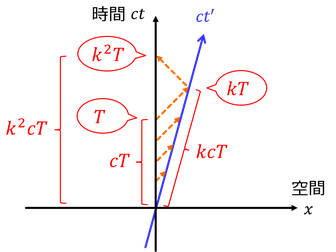
　静止している慣性系Sの光源Aから、移動している慣性系S'の観測者Bに向かってしばらく光を送り続ける。この時間をT，Bが受け取り続ける時間をk倍のkTとしよう。また、Bは光を受けるとすぐにAへ送り返していたとする。すると、AがBから光を受け取り続ける時間は、ｋ倍の(k^2)Tとなる。

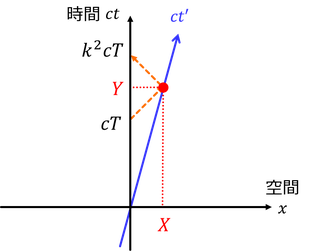
　Bが光を受け取り終え、最後の光をAに送り返したときの点を、慣性系Sの時空図上で求めよう。この座標を(X，Y)とすると、

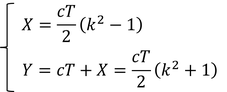
図からこのように求めることができる。ここで、慣性系S'の時間軸の傾きがc/vであることを思い出せば、

より、

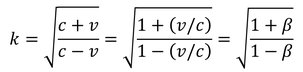
こうしてｋの値が得られる。ただし、

とおいた。

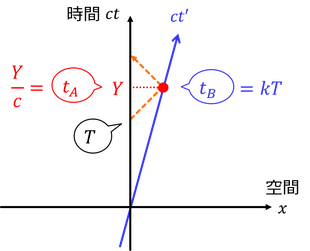
　次は、Bが光を受け取って、最後の光を放射した瞬間の時刻をA，Bそれぞれの慣性系で求める。AにとってはY/cであり、BにとってはkTである。いま求めたｋを使って書き直すと、

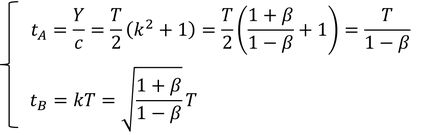
となる。これらの関係は、

である。この式は、

Aの時計はBの時計よりも進んでいる。
Bの時計はAの時計よりも遅れている。

と言える。つまり、動いている人の時計は、静止している人の時計よりもゆっくりと進み、時間が延びるのだ。

　具体例を挙げる。地球上には宇宙から多くの粒子がやってきているが、上空20kmのところでミューオンという粒子が生まれている。ミューオンの中には光速の99.995%という速さのものもあるが、ミューオンは2×10^(-6)秒で別の粒子に変わってしまうため、地上に到達することはできない。

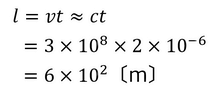
しかしミューオンは地上にやって来ている。その理由が、今回のテーマである「時間の延び」だ。β＝0.99995として計算すると

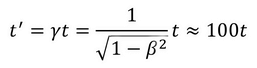
となる。これは、ミューオンの時間は地上から見ると100倍に延びているように感じるということ。だから

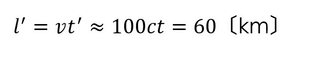
距離も100倍進むことができることが分かる。こうしてミューオンは地上に到達することができるのだ。