世界間隔
時間や空間は相対的なものである。動いているものの時間は延び、動いているものの空間は縮む。しかし、変わらないものもあるのだ。今回はそれを紹介しよう。
ガレージのパラドックス

いま、長さがLのガレージと、それよりも長い長さL0(>L)の自動車があるとする。ガレージよりも自動車が長いので静止状態だと収まらないが、動いている自動車はローレンツ収縮によって縮むので、収まることができる。しかし、自動車側からみるとガレージの方が縮むので収まらない。どういうことだろうか。この問題を「ガレージのパラドックス」という。

時空図を使って考えてみよう。地上から見ると自動車が動いていて、時刻0においてちょうど自動車がガレージに収まったとする。このとき、間違いなく自動車はガレージに収まっている。

では”このとき”自動車から見たとき、自動車はガレージに収まっているのだろうか。問題は”このとき”が地上と自動車で異なることだ。自動車の前端は移動するし、後端の位置も移動するわけだが、前端の位置と後端の位置の”同時”が地上と自動車で異なるのだ。時空図で見てもらえば分かるように、自動車側の時計で後端がガレージの入り口に達したときを時刻t'=0とすると、この時刻において自動車の前端はすでにガレージの出口を通過した後になっていいるわけなのだ。だから、自動車にとって、自動車はガレージに収まらない。
同時が地上と自動車で異なるので、地上側と自動車側で自動車がガレージに収まったり収まらなかったりしても、それは矛盾ではないのだ。
世界間隔
次は距離について考えよう。距離x2-x1は、ガリレイ変換
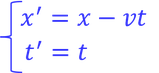
に対して、

このように形を変えない。しかし、ガリレイ変換は時間の相対性を考えられていない。そこで、時間も含んだ座標変換であるローレンツ変換

を考える必要がある。すると、距離x2-x1は、ローレンツ変換に対して、
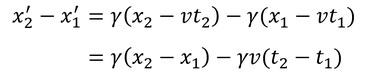
このように形を変えてしまう。
では、ローレンツ変換に対して形を変えない時空図上の「距離」が考えられないだろうか。そこで、

という量を導入する。これを「世界間隔」と呼ぶ。この量は、ローレンツ変換に対して、

このように形を変えない。世界間隔は「不変間隔」とも呼ばれる。いまは空間としてx軸のみを考えたが、y軸,z軸方向も考えると、世界間隔は

と書ける。
光円錐

世界間隔は時空図上でイメージしておくといい。すぐに時間軸方向の幅と空間軸方向の幅の差になっていることに気付けるはずだ。世界間隔の2乗が0のときは、時間軸方向の幅と空間軸方向の幅が等しいことを示しており、時空図上では斜め45°の直線状の2点の間隔ということになる。これを「光的」と呼ぶ。
世界間隔の2乗が負のときは、時間軸方向の幅が空間軸方向よりも広いことを示しており、その2点は「時間的」な関係にある。
世界間隔の2乗が正のときは、空間軸方向の幅が時間軸方向よりも広いことを示しており、その2点は「空間的」な関係にある。
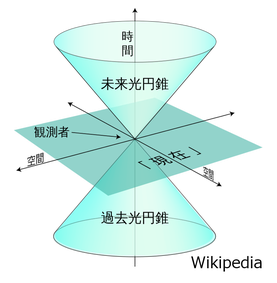
空間軸を2つにすると、上のような円錐が書ける。これを「光円錐」と呼び、光円錐の表面が「光的」、その内部が「時間的」、その外が「空間的」な関係になっている。光円錐の内部は時間的に移動が可能な領域であり、これを「因果的領域」ともいう。
固有時間

慣性系Sに対して速度vで運動している物体があるとする。時間と空間の変化量をそれぞれdt,dx,dy,dzとすると、世界間隔の2乗は

と書ける。ここで、速度vは
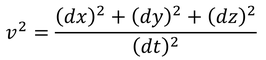
だから、
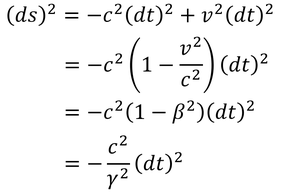
と変形できる。

続いて、慣性系Sに対して速度vで運動する物体の速度が0になるような慣性系S'を考える。慣性系S'における世界間隔は、dx'=dy' =dz'=0だから、
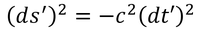
となる。ここで、世界間隔は慣性系に寄らず一定であることから
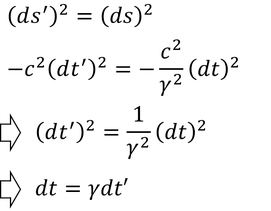
時間の延びが得られる。

それぞれの慣性系とともに運動する時計が刻む時間を、それぞれの慣性系における「固有時間」という。いま、慣性系S'の固有時間をτとする。すなわちdτ=dt'である。すると、世界間隔の式から
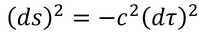
世界間隔と固有時間の関係式が得られる。世界間隔がローレンツ変換に対して形を変えなかったから、固有時間もローレンツ変換に対して形を変えないことが分かる。
