熱機関の効率

気体に熱を加えると、気体は膨張する。膨張するということは、この気体は外部に対して仕事をするということだ。この性質を利用して、熱を仕事に変える装置のことを熱機関という。また、熱機関の効率のことを熱効率という。詳しく見ていこう。
気体がした仕事
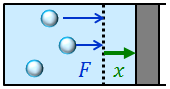
容器内の気体がピストンを押して外向きに動かしたとき、気体が「仕事をした」という。前回はこれを体積変化と対応させただけだったが、今回はきちんと計算してみよう。
簡単のために、はじめは圧力pが一定の定圧変化を考える。気体がピストンを力Fで押して、ピストンがxだけ移動したとすると、このとき、気体がした仕事Wは、

である。ここで、気体の圧力p, 容器の断面積をSとすると、F=pSだから、
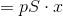
また、このとき増えた気体の体積はΔV=Sxだから、

になる。つまり、気体がした仕事は「圧力×体積変化」で計算することができるということだ。
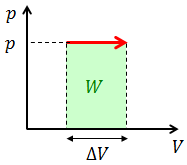
この内容をp-Vグラフに表すと上のようになる。気体がした仕事はp-Vグラフの面積として表されるのだ。また、グラフの面積が定積分だったことを思い出すと、一般的に、気体がした仕事Wは次のように表されることが分かる。
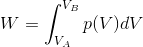
この式は定圧変化によらない。
問題
温度Tを維持したまま気体を加熱すると、この気体の体積はVA→VBと変化した。このとき気体がした仕事Wを求めよ。
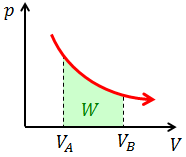
解答
気体の状態方程式「pV=nRT」より、圧力pは
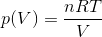
と表すことができる。いま、温度Tが一定なので変数は体積Vだけである。あとは、これをVA~VBの範囲で積分すれば、
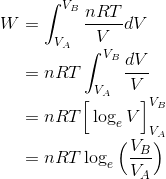
となる。
熱サイクル
気体を加熱して仕事をさせた後、何らかの方法でもう一度元の状態へ戻してやれば、何度も繰り返し気体に仕事をさせることができる。

ただし、気体が外部へした仕事W(+)よりも気体が外部からされた仕事W(-)が小さくなければ、全体として仕事を取り出すことができないので、少し工夫が必要だ。

このような気体の状態の繰り返しを熱サイクルといい、1サイクルによって取り出すことのできる仕事Wは、

である。また、熱サイクルによって気体から繰り返し仕事を取り出す装置を熱機関という。熱機関には、蒸気機関やガソリン機関などがある。
熱効率
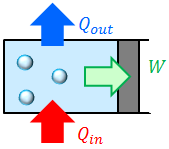
熱サイクルの間に、気体が吸収した熱量をQ(in)、気体が放出した熱量をQ(out)、全体として気体がした仕事をWとすると、これらのあいだには

という関係がある。これは、
-
熱機関は吸収した熱量Q(in)のうち一部を仕事Wに変え、残りQ(out)を捨てている。
ということを意味している。
ところで、より良い熱機関とはどのようなものかというと、やはり熱をどれだけたくさん仕事に変えられるかだろう。そこで、熱機関が吸収した熱量Q(in)と実際にした仕事Wの割合を考えて、

これを比較してやればいい。これを熱効率という。
問題
500Jの熱量を吸収して425Jの熱量を放出する熱機関がある。この熱機関の効率eを求めよ。
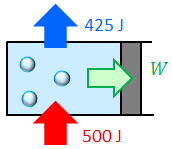
1サイクルの間にこの熱機関がする仕事Wは

だから、熱効率eは
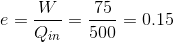
よって、15%ということになる。
