熱力学第2法則
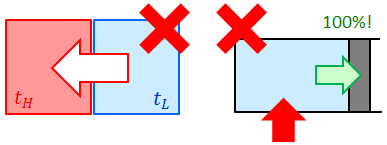
熱は高温物体から低温物体へと移動し、低温物体から高温物体へ“勝手に”移動するということはない。このきまりを熱力学第二法則という。
熱効率100%の熱機関を作ることはできない。つまり、吸収した熱をすべて仕事に変えることはできない。このきまりも熱力学第二法則という。
同じ名前なので、前者をクラウジウスの原理、後者をトムソンの原理と呼ぶことにする。異なる内容に感じるが、どうしてどちらも熱力学第二法則と呼ばれているのだろう。
可逆変化と不可逆変化
冷凍庫から氷を出してしばらく置いておくと、やがて融けて水になる。勝手に氷に戻るということはない。水平な机の上で消しゴムをはじくと、少しすべってから摩擦によってやがて止まる。その後、勝手に動き出し、再び手に戻ってくるということはない。このような変化を不可逆変化という。一般に、熱が絡む現象はすべて不可逆変化である。
これに対し、外部へ何の影響も与えず、元の状態へと戻すことができる変化を可逆変化という。例えば、空気抵抗や支点の摩擦が無視できる振り子は可逆変化といえる。
準静的過程
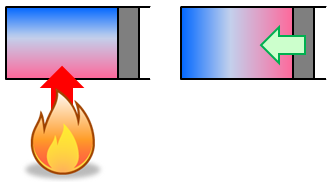
容器に入った気体を加熱すると、加熱された側の気体の温度が上がり、容器内の熱平衡状態が崩れてしまう。また、容器に入った気体を圧縮しても、外力を加えた側の気体の温度が上がり、熱平衡状態が崩れてしまう。
それでは熱平衡状態を保ったまま、気体を加熱したり、圧縮したりするにはどうすればよいのかといえば、熱平衡状態が崩れないよう、“きわめてゆっくりと”状態を変化するしかない。この、“きわめてゆっくりと”した理想的な変化の過程を準静的過程と呼ぶ。
これに対し、途中で熱平衡状態が崩れてしまう変化のことは緩和過程と呼ぶ。熱平衡ではない状態というのは非常に複雑な状況になっていて、それと全く同じ状態を2度と再現することができない。そのため、再び同じ過程をたどることはできないし、もちろん逆にたどることもできない。つまり、不可逆変化である。

実は、これまで考えてきた気体の状態変化は、すべて可逆変化であり、準静的過程を考えていた。熱平衡状態でなければ気体の状態量が決められず、p-Vグラフ上に記すことはできないためである。今後、可逆過程Cと不可逆過程Xを区別する必要がある場合は、これを実線と点線で描き分けることにしよう。
カルノーサイクル

さて、次は準静的過程について少し具体的にその方法を考えてみよう。まず、”きわめてゆっくりと”体積を変化させようと思ったら、ピストンをゆ~っくりと移動させればいいことは分かる。それでは、”きわめてゆっくりと”温度を変化させるためにはどうすればよいのだろう。
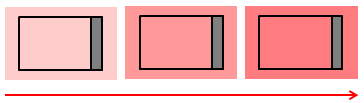
答えは、微妙に異なる温度の熱源をたくさん用意して、順番に気体を接触させていくこと。理想的には、無限大個の熱源が必要になるので、可逆な定圧変化や定積変化を実現させることは大変なことなのだ。
ただし、断熱変化の場合にはもちろん熱源は要らないし、等温変化の場合には、1つの熱源に接触させながらゆっくりと体積を変化させることで実現させることができる。ということは、等温変化と断熱変化だけで熱サイクルを実現させることができるならば、温度の異なる2つの熱源だけで熱機関が完成することになる。

この熱サイクルはカルノーサイクルと呼ばれ、非常に重要なのでよく覚えておこう。この他にも可逆な熱サイクルはいくつも考えられるが、2つの熱源だけで実現可能な熱サイクルはこれだけだ。
① 高温熱源のもとで等温膨張
② 断熱膨張(温度は下がる)
③ 低温熱源のもとで等温圧縮
④ 断熱圧縮(温度は上がる)
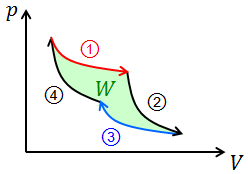
p-Vグラフは図のようになり、きちんと仕事Wが取り出せていることが分かる。
熱力学第二法則
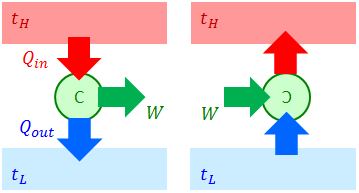
カルノーサイクルのポイントは2つある。2つの熱源だけで動かすことができるという点と、可逆変化だから逆サイクルを考えることができるという点だ。逆サイクルでは、仕事を与えることによって低温熱源から高温熱源へ熱を運ぶことができる。
さぁ、これをうまく使って、冒頭で紹介した2つの原理が等価な熱力学第二法則であることを証明しよう。
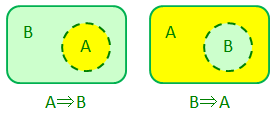
この証明には対偶法を用いる。これは、「AならばB(A⇒B)」を証明するために、「BでないならAでない(B×⇒A×)」を証明するという方法だ。左上が「A⇒B」の図で、Aの領域であればBの領域でもあるということを意味している。このとき、Bの領域に含まれていなければAの領域にも含まれていないので、「B×⇒A×」ということも成り立っていることが分かる。
また、「A⇒B」が成立して、同時に「B⇒A」が成立するならば、これはAとBが全く同じ内容であることを示している。上の図で言うと、Aの領域とBの領域がピッタリ重なるということだ。ちなみにこれを「A⇔B」と表現したりもする。
だから方針はこうだ。
① クラウジウスの原理 ⇒ トムソンの原理を対偶法で証明
② トムソンの原理 ⇒ クラウジウスの原理を対偶法で証明
これができれば、クラウジウスの原理とトムソンの原理が等価であることを証明できたことになる。
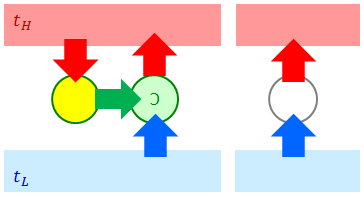
① クラウジウスの原理 ⇒ トムソンの原理
「トムソンの原理×⇒クラウジウスの原理×」を示す。まず、トムソンの原理を否定するということは、熱効率100%の熱機関が存在するということなので、この熱機関(上図の黄色)を高温熱源に接続する。そして、この機関から取り出した仕事を受け取って低温熱源から高温熱源へ熱を送るように、逆カルノーサイクルを接続してやる。すると、全体として、仕事を与えてやることなしに低温熱源から高温熱源へと熱が運ばれてしまうことになる(上図右)が、これはクラウジウスの原理に反している。よって①が証明できた。

② トムソンの原理 ⇒ クラウジウスの原理
「クラウジウスの原理×⇒トムソンの原理×」を示す。まず、クラウジウスの原理を否定するということは、低温熱源から勝手に高温熱源へ熱が運ばれるということである。この性質を利用して、カルノーサイクルから棄てられた熱をすべて高温熱源へ戻してやれば、全体として熱効率100%の熱機関ができる(上図右)が、これはトムソンの原理に反している。よって②が証明できた。
以上より、トムソンの原理とクラウジウスの原理が同様の内容であることが証明できた。
