内部エネルギー
熱力学第一法則のときに登場した内部エネルギー。そのときは、絶対温度Tに比例する物理量であることしか話さなかった。今回は気体の分子運動の側面から、その実態に迫っていこう。
気体の圧力

一辺の長さが L の立方体の容器に入った、気体の分子運動を考える。いま、質量 m の気体の分子が、速度 v で内壁Sと弾性衝突したとする。この分子が内壁Sから受けた力積 i は、速度の内壁Sに垂直な成分を vxとすれば、運動量と力積の関係より、


と計算できる。
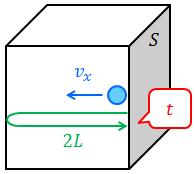
また、内壁Sと衝突したこの分子が、1往復して再び戻ってくるまでの時間 t は、
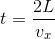
である。これはつまり、t 秒間に1回の割合で内壁Sと衝突するということで、⊿t 秒間の衝突回数 j は、
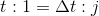

になる。よって、この気体の分子が、⊿t秒間に内壁Sへ与える力積の大きさ(I=i×j)は、

と分かる。すると、この式と力積の定義式「I=f⊿t」を比較することで、この気体の分子が内壁Sへ与える平均の力
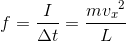
を求めることができる。
これまでは1個の分子だけを考えてきたが、ここからは容器内に含まれるN個の分子全体を考えよう。f の平均値を

と表せば、N個の分子が内壁Sへ与える力の総和Fは、
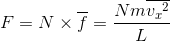
となる。また、この式には速度のx成分が含まれているが、この値は、座標軸の取り方によって異なるので都合が悪い。そこで、軸の取り方によらないvを使ってこの式を表すことを考えよう。ベクトルの合成および対称性から、

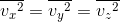
と仮定すると、
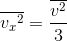
となるから、これを使ってFを書き変えることができる。

以上より、容器内の気体の圧力「P=F/S」は、
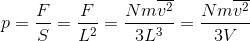
となる。ただし、体積V=L3とした。
エネルギー等分配の法則
次は、気体の分子が持つ運動エネルギーの平均値

を求めよう。さっき導いた圧力の式と気体の状態方程式「pV=nRT」を比較すれば、
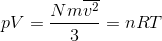
だから、


となる。ここで、物質量n[mol]と気体の分子数N[個]の関係N/n=6.0×1023[個/mol]を思い出そう。これをアボガドロ数という。これをNAと表すと、

となる。ここで、”分子1個あたりの気体定数”

をボルツマン定数という。熱力学と統計力学とを結びつける大切な定数である。
さて、これで気体分子の平均運動エネルギーが
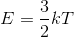
と表せることが分かったが、ここで、この式の中の「3」という数字に注目して欲しい。これは、この分子の運動の自由度が「3」であるということを表している。運動の自由度とは、運動の様子を表すために必要な変数の数のことで、自由度が3というのは x,y,z の3方向へ自由に動けるという意味だ。
これまでに考えてきた、1つの分子が1つの原子からなる気体を単原子分子気体とよぶ。対して、2つの原子が結合し、1つの分子になっている気体を二原子分子気体とよぶ。
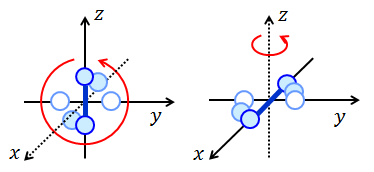
二原子分子気体の場合は、x,y,z の3方向への並進運動のほかに、2種類の回転運動を考えることができるので、運動の自由度は「5」である。よって、二原子分子気体の平均運動エネルギーは、
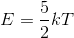
となる。
このように、1自由度あたり(1/2)kTのエネルギーが等しく分配されているというきまりをエネルギー等分配の法則という。
気体の内部エネルギー
さあいよいよ気体の内部エネルギーUを求めよう。気体の分子はそれぞれ運動エネルギーを持っている。容器内のすべての気体について、この運動エネルギーの総和を計算する。これが、気体の内部エネルギーだ。ボルツマン定数は k=R/NA=nR/N だから、
単原子分子気体の内部エネルギー

二原子分子気体の内部エネルギー

- 物体を構成している実際の分子は、運動をしながら、互いに影響を及ぼし合っている。そのため、この分子間力による位置エネルギーなどを含める必要があるのだが、高校の範囲ではこれを無視する。
