モル比熱

質量m[g]の物体を加熱したとき、加えた熱量Q[J]とその温度変化の⊿T[K]のあいだには、
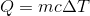
という関係がある。この c [J/(g・K)]を比熱という。
ところで、この式はm[g]の代わりに物質量n[mol]を使ってもいい。すると、
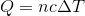
となる。このときの c [J/(mol・K)]をモル比熱という。
- 高校物理では、「Q=mc⊿T」の方は固体や液体、「Q=nc⊿T」の方は気体について使われる場合が多い。
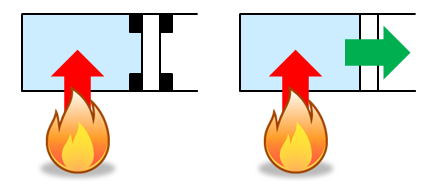
ところで、気体の温度変化は、その変化のさせ方によってずいぶん違う。例えば、体積の変わらない定積変化(左図)よりも、熱量の一部が体積増加に使われてしまう定圧変化(右図)の方が温度は上がりにくいだろう。そこで、これらのモル比熱には、それぞれ
- 定積モル比熱cV…定積変化のときのモル比熱
- 定圧モル比熱cp…定圧変化のときのモル比熱
という特別な名前が付いている。これらの記号を使うと、気体が吸収した熱量は、それぞれ
- 定積変化の場合
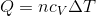
- 定圧変化の場合
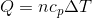
と表すことができる。
定積変化
定積変化では
- 気体が吸収した熱量 Q=ncV⊿T
- 気体がした仕事 W=0
だから、気体の内部エネルギーの増加量を⊿Uとすると、熱力学第一法則の式から、
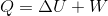


と求めることができる。
ここで、前回導いた気体の内部エネルギーの公式を思い出そう。
- 単原子分子…U=(3/2)nRT
- 二原子分子…U=(5/2)nRT
物質量nが一定であれば、“内部エネルギーUの値は温度Tだけで決まる”ということが分かる。だから、もちろん内部エネルギーの変化⊿Uの値も、温度変化⊿Tのみによって決まり、
- 単原子分子…⊿U=(3/2)nR⊿T
- 二原子分子…⊿U=(5/2)nR⊿T
という関係が成り立っていることになる。この式とさっきの「⊿U=ncV⊿T」を比べることで、
- 単原子分子気体の定積モル比熱 cV=(3/2)R=12.465
- 二原子分子気体の定積モル比熱 cV=(5/2)R=20.775
を求めることができる。(※気体定数R=8.31[J/(mol・K)])
定圧変化
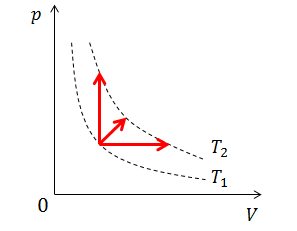
改めて強調しておこう。“内部エネルギーUの値は温度Tだけで決まる”。だから、内部エネルギーの変化⊿Uの値は、温度変化⊿Tだけで決まる。そして、

と表すことができる。式の中に定積モル比熱cVが含まれているが、この式は定積変化に限らないということに注意しよう。温度変化が同じ⊿Tであれば、定積変化だろうが定圧変化だろうが、すべて同じ式で書けるのだ(上図)。
さて、ここからは定圧変化について考えよう。まず、内部エネルギーの変化量ΔUは上記のように表すことができる。続いて、気体が吸収した熱量Qは、

である。最後に気体がした仕事Wは、定圧変化の場合、気体の圧力をp, 体積変化を⊿Vとして「W=pΔV」だったから、
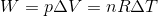
となる。気体の状態方程式を用いた。
さて、ここまでの結果を熱力学第一法則の式に代入すると、



というモル比熱どうしの関係式を得ることができる。これを、マイヤーの関係式という。
マイヤーの関係式を使うと、定圧モル比熱は、
- 単原子分子気体 cp=cV+R=(5/2)R=20.775
- 二原子分子気体 cp=cV+R=(7/2)R=29.085
(※気体定数 R=8.31[J/(mol・K)])
となる。
ポアソンの式
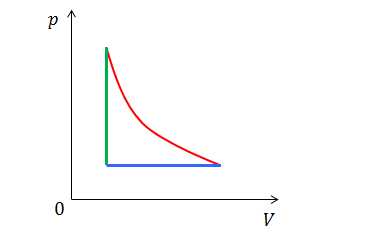
気体の状態変化を表すp-Vグラフについて、次の3種類は簡単に描くことができるが、断熱変化は難しい。
- 定積変化…p軸に平行 (V=一定)
- 定圧変化…V軸に平行 (p=一定)
- 等温変化…反比例 (pV=一定)
そこで、正確なp-Vグラフを表すために、断熱変化を示す式を求めてみよう。
微小量に対する熱力学第一法則の式「d'Q=dU+d'W」を使う。この式へ
- d'Q=0
- dU=ncVdT
- d'W=pdV=(nRT/V)dV
を代入して計算すればいい。断熱変化の場合、3つも変数(p,V,T)があるので、気体の状態方程式を使って、pを(V,T)で表すことで変数を1つ減らしてある。

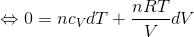

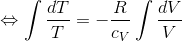
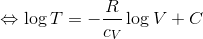
ここで、R=cpーcVだから、
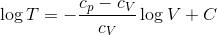
となる。さらにγ=cp/cVとおく。これを比熱比という。


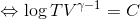

右辺のeCは定数なので、TVγー1の値は常に一定という関係が分かった。さらに、気体の状態方程式を使ってTを消去しよう。
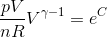

nが一定ならば、右辺のnReCは定数なので、pVγの値は常に一定ということが分かった。以上の、
-
TVγ-1=一定
- pVγ=一定
をまとめてポアッソンの式という。断熱変化のときは、ボイルの法則やシャルルの法則と同じようにこれを使おう。
