波と振動

音の性質 ←→ ドップラー効果

　地震が起こると建物が揺れる。このとき、ゆっくりとした地震ほど大きな建物が揺れることが知られている。このように、物体ごとの自然な振動を固有振動と呼び、揺れの周期を固有周期、振動数を固有振動数という。そして、固有周期に合わせて外部から力を受けると、建物は大きく揺れることになる。この現象を共振(音の場合は共鳴)という。

　弦をはじくと、その長さや張力の強さごとに異なる音が出る。これは、色々な種類の定常波がその度ごとに異なる割合で混じりあっているからである。

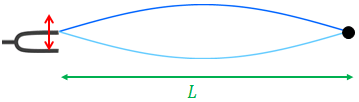
　例えば、弦を振動させて、図のような形の定常波ができたとする。このもっとも単純な形の定常波を作る振動を基本振動と呼び、発生する音を基本音と呼ぶ。このときの振動数f1を求めてみよう。

　弦の長さがLのとき、この形の定常波を作る元の波の波長λ1は

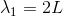
である。すると、弦を伝わる波の速さがvのとき、振動数f1が波の基本式「v=fλ」を使えば、

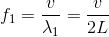
と計算できる。

　続けて振動数を変化させると、図のような定常波ができることがある。この振動を2倍振動と呼び、発生する音を2倍音と呼ぶ。2倍振動では、元の波の波長λ2は弦の長さLと一致する。

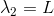
だから、振動数f2は、

である。

　続いて3倍振動のときの振動数f3を求めよう。このときの音を3倍音と呼ぶ。元の波の波長λ3は弦の長さLの2/3である。

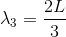
だから、振動数f3は、

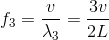
である。

　4倍振動以降も、同じように①定常波の図を描いて、②図から波長を読み取って、③波の基本式「v=fλ」を使うと振動数が求められる。一般的に、基本振動以外の定常波が作る音を倍音と呼ぶ。

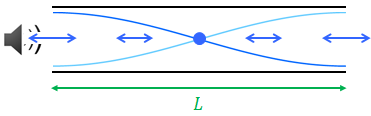
　続いて気柱の開口部ににスピーカーを当てて、空気を振動させることを考える。両端が開いた管を開管という。いま、図のように開口部が腹となるような定常波が生じたとする。このような最も簡単な定常波の形を基本振動という。

　基本振動のときの振動数f1を求めよう。気柱の長さをLとすると、この定常波を作る元の波の波長λ1は

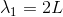
である。だから、音速をVとすると、振動数f1が

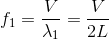
となる。

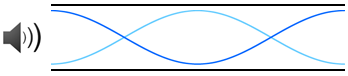
　続いてスピーカーの音を調節し、図のような定常波が発生したとする。このときの振動を2倍振動という。基本振動と同じ形が2つあることからこの名前になっている。2倍振動のとき、元の波の波長λ2は気柱の長さLと等しい。

だから、振動数f2は、

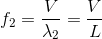
となる。

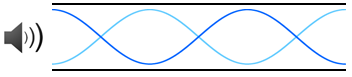
　図のような定常波を作る振動を3倍振動という。基本振動と同じ形が3つあることが分かる。このとき、元の波の波長λ3は気柱の長さLの2/3だから、

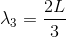
振動数f3は、

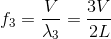
となる。

　弦の振動も含めて、振動数を求めるために、①定常波の図を描いて、②図から波長λを読み取って、③計算によって振動数ｆを求める、という手順をしっかり身に付けよう。

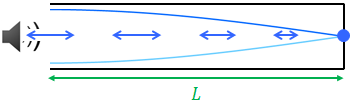
　続いて、片方が閉じた閉管について考える。このとき、開口部から音を当てると、図のような基本振動となる。閉じた方は定常波の節になっていることが分かるだろう。このとき、管の長さLを使うと、元の波の波長λ1はLの4倍となる。

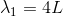
音速をVとすると、振動数f1は、

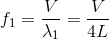
となる。

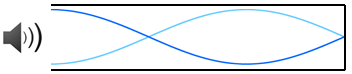
　さて、一方が腹、他方が節となる定常波には上図のような形もある。この中には、基本振動の形が左右逆向きのものも含めて3つ存在しているため、この振動は3倍振動と呼ばれる。2倍振動は存在しないので気を付けよう。このとき、元の波の波長λ3は

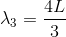
だから、振動数f3は

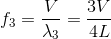
となる。

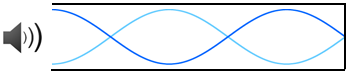
　3倍振動の次は5倍振動だ。2倍や4倍だと、閉じている側が定常波の節にならないだろう？ このとき、元の波の波長λ5は、

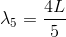
であり、振動数f5は

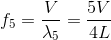
となる。

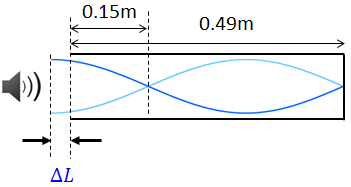
　ところで、実際に実験してみると開口部が定常波の腹から少しだけずれてしまうことがある。このずれΔLを開口端補正という。そのため、3倍振動であっても、単純に管の長さの4/3倍によって波長を見積もってはいけない。この図の場合、基本振動となるときの管の長さが0.15m，3倍振動となるときが0.49mだから、その差を取ることで波長の1/2の長さが計算できる。ここから波長λを求めなければならない。

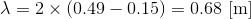
ここで音速をV=340m/sとすると、音の振動数fが、

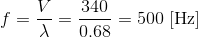
と求められる。