運動の法則
アイザック・ニュートンは1687年、『自然哲学の数学的諸原理(プリンキピア)』という書籍で運動の法則および万有引力の法則を公表した。運動の法則はさらに3種類の法則から成り立っており、順番に①慣性の法則、②運動の法則、③作用反作用の法則と呼ばれている。
慣性の法則

電車が発進するとき、身体が後ろに傾いて転びそうになる。また、電車が停車するときは、身体が前に傾いて転びそうになる。これは、身体が「静止」や「等速直線運動」という今の運動を維持しようとするためだ。この性質を慣性と呼び、「物体に力がはたらかないか、はたらいていてもその力がつり合っている場合には、静止している物体は静止をし続け、運動している物体は等速直線運動を続ける」というきまりを慣性の法則という。
慣性の法則には4つの内容が含まれている。
- 力がはたらかないとき、物体は静止し続ける。
- 力がはたらかないとき、物体は等速直線運動を続ける。
- 力がつり合っているとき、物体は静止し続ける。
- 力がつり合っているとき、物体は等速直線運動を続ける。
だから、慣性の法則を説明せよと言われたら、上の4つの内容をきちんと含んでいる文章を書く必要があるので気をつけよう。
運動の法則

次は、物体にはたらく力がつり合っていない場合を考えよう。このとき、物体は合力の向きに加速する。例えば、右向きに5N、左向きに2Nの力がはたらいているとき、その物体は右向きに加速していくというわけだ。
簡単な実験をしてみると、物体に生じる加速度の大きさaは、与える力Fの大きさに比例し、物体の質量mに反比例することが分かる。これを運動の法則という。式に表すと次のようになる。
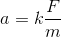
よく分からなければ、Fを2倍, 3倍にしたとき、aも2倍, 3倍になること、それからmを2倍, 3倍にしたとき、aは1/2倍, 1/3倍になっていくことを確認してみよう。前者の関係を比例、後者の関係を反比例というのだった。
ところで、今の式を書き換えると、
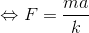
になる。ここで、この式へm=1, a=1を代入してみるとF=1/kという値になるが、どうせならk=1として、m=1, a=1のときの力の大きさをF=1と決めてしまった方がなにかと便利そうだ。

つまり、「1kgの物体に1m/s2の加速度を生じさせる力」を"1"としようというわけで、現在ではこれは1Nと決められている。
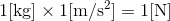
また、元の式をk=1として書き換えた式
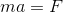
を運動方程式という。運動方程式は、高校物理、いや世の中の物理公式の中で1番と言ってもいいほど大切な式だ。必ず使いこなせるようになろう!
運動方程式
(1) 2kgの物体に3Nの力を加えたときに生じる加速度の大きさaを求めよ。
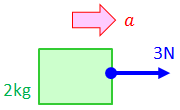
→運動方程式(ma=F)より、
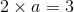
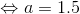
よって、答えは1.5m/s2
(2) 2kgの物体を右向きに3N, 左向きに2Nで引っ張ったとき、生じる加速度の向きと大きさを求めよ。
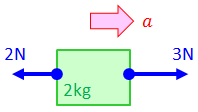
→右向きを正として、運動方程式(ma=F)より、

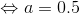
よって、答えは右向きに0.5m/s2
- 力が2つ以上ある場合、右辺は(加速度と同じ向きの力)ー(加速度と逆向きの力)となる。
(3) 質量mの物体が傾き30°のなめらかな斜面上を運動している。このとき物体に生じている加速度の大きさaを求めよ。
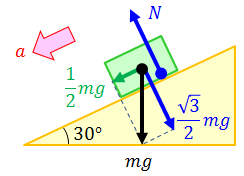
→斜面方向下向きを正とする。運動方程式より、
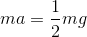
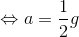
よって、答えは(1/2)g
- 加速度の向きに対して”斜めの力”がある場合には、それを分解して考える必要がある。
(4) 角度30°のあらい斜面上を質量mの物体が下向きに運動している。このときの加速度の大きさaを求めよ。

→物体にはたらく動摩擦力の大きさf'は、
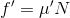
と表せる。また、斜面に垂直は方向の力はつり合っている必要があるので、力のつり合いより、
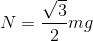
よって、運動方程式(ma=F)を立てて解けば、
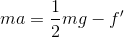

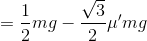
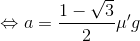
となる。
- 今のように、運動方向と、運動方向に垂直な方向と、2種類の式を作る必要がある場合もある。式が足らない!と思ったら、垂直な方向に目を向けてみよう。
(5) なめらかな面上に質量Mの物体に糸を付け、滑車を通して質量mの物体につないだ。このとき、それぞれの物体に生じている加速度の大きさaと、糸の張力の大きさTを求めよ。

→物体が2種類あるので、運動方程式を2つ作る。ma=Fより
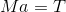
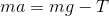
この2つの式を連立させてaとTについて解けば、


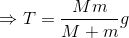
となる。
- 2つ以上の物体が力を及ぼし合っている問題の場合、まとめて考えて1つの運動方程式を作るのではなく、物体の数だけ運動方程式を作って連立方程式を解くようにしよう。
