浮力と摩擦力
前回、重力mg, 垂直抗力N, 摩擦力f, 張力T, 弾性力kxという5つの力を紹介した。今回は、多くの高校生がつまずく浮力と、摩擦力についての詳しい内容を考えよう。
圧力

体重計に片足で乗っても目盛りは変わらない。これは、片足で乗っても「人が体重計を押す力」に変化はないと言うことだ。ところが、鉛筆を縦に指で挟むと、加わる力の大きさは同じはずなのに尖っている方が痛い。どうやら、接触面積によって効果が変わってくる場合もあるようだ。
そこで、力F[N]と接触面積S[m2]を考えて、「1m2の面積あたりにはたらく力」という量を導入しよう。
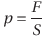
これを圧力といって、[Pa(パスカル)]という単位を使う。力F[N]が大きいほど圧力p[Pa]も大きく、また接触面積S[m2]が小さいほど圧力p[Pa]は大きい。つまり、尖っている側の方が指との接触面積が小さいから圧力が大きく、痛いと感じるわけだ。
水圧
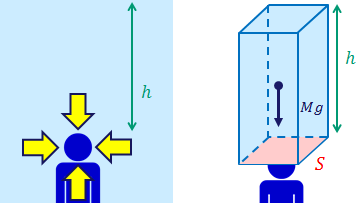
水中に潜っていくと次第に大きな水圧を感じるようになる。水圧は深さに比例し、どの向きからも同じ大きさである。
水深h[m]における水圧p[Pa]は、頭の上の水の重さを考えることで求められる。頭の面積をS[m2]、頭上の水の重さをMg[N]とすると、

となる。
ここで、水の密度ρ[kg/m3]を考えよう。密度とは「1m3あたりの質量」のことで、体積をV[m3]、質量をm[kg]とすると、
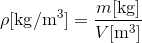
と表すことが出来る。ちなみに密度を表す記号ρはローと読む。この記号を使って今の式を書き換えると、質量はm=ρVだから、

になる。いま、頭上にある水の体積V[m3]は、頭の面積S[m2]と水深h[m]を使って、
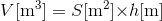
と表すことができるから、水深h[m]における水圧p[Pa]は、
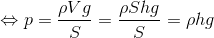
ということになる。結果的にSが消えてしまったことから、水圧は、圧力なのに面積S[m2]によらないということがわかる。
浮力
水中に物体を沈めると、この物体は水から鉛直上向きに力を受ける。この力を浮力という。浮力を水圧で説明してみよう。

いま、水中に底面積S[m2]、高さh[m]の直方体を沈めたとする。直方体の上面の水深をh1[m]、下面の水深をh2[m]とすると、それぞれの水深における水圧p1[Pa], p2[Pa]は、
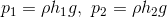
になっている。
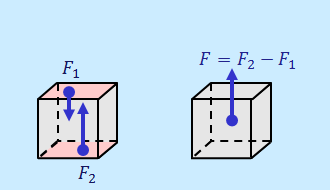
また、圧力の定義「p=F/S」より、圧力pと接触面積Sが分かれば、その面にはたらく力の大きさF=pSを求めることができるので、水中の直方体の上面と下面に水が与えている力の大きさF1[N], F2[N]は、
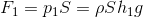

であることが分かる。F1は水が直方体の上面を下向きに押す力で、F2は下面を上向きに押す力(F2>F1)なので、結果的に、この直方体は水からこれらの力の差F=F2-F1を受けていることになる。これが浮力だ。計算すると、
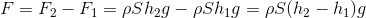
また、水深の差(h2-h1)[m]はこの直方体の高さh[m]に等しいから、
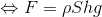
であり、Sh[m3]は水中に沈んでいる直方体の体積に等しいから、これをV[m3]とすると、
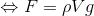
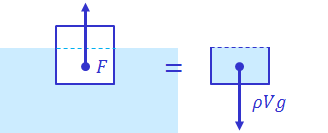
ということになる。
さて、この式を公式とみなせば「浮力はρ×V×gで計算できる」というただそれだけの意味なのだが、この式を「浮力(F)は〇○力(ρVg)に等しい」と解釈してみよう。公式ではなく、関係式だと考えるわけだ。では、"〇○力"とは何だろう。
そういえば、「ρV=m[kg]」だった。ということは、ρVg=mgではないか。これは水の重さだ。特に、"水中の物体と同じ体積Vの"水の重さを意味している。つまり浮力F[N]は、物体が"押しのけた"水の重さρVg[N]に等しいというわけ。これをアルキメデスの原理という。

ただし、水に浮いている氷のように、物体が完全には水中に沈んでいない場合は要注意! アルキメデスの原理によると、浮力は物体が「押しのけた」水の重さに等しいわけだから、水中に「沈んでいる部分」の体積を考えるだけでいい。
ところで、浮力は水中だけでなく、あらゆる気体や液体の中ではたらく。気体や液体を総称して流体と呼ぶので、この流体という言葉を使ってアルキメデスの原理を言い換えると、「流体中の物体にはたらく浮力の大きさFは、その物体が押しのけた流体の重さρVgに等しい」となる。
- 浮力では、「F=ρVg」を公式としてただ暗記するだけでなく、アルキメデスの原理と合わせてきちんと理解できているかどうかがポイントだ。
摩擦力
摩擦力には2種類あり、物体が静止している場合の摩擦力を静止摩擦力、動いている場合を動摩擦力という。それぞれ求め方が違うので、しっかりと区別して覚えよう。
まず、物体が静止しているときには、物体にはたらく力がつり合っているわけだから、静止摩擦力は力のつり合いを利用して求めることができる。物体が動いている場合には、力がつり合っているとは限らないので、次の公式を使う。動摩擦力をf'[N]、垂直抗力をN[N]として、

動摩擦力は垂直抗力に比例しているという意味。この比例定数μ' (ミューダッシュ)を動摩擦係数という。
- 静止摩擦力f[N]は、力のつり合いで求める。
- 動摩擦力f'[N]は、公式で求める。

物体にF[N]の力を加えていくと、Fが小さいときは静止摩擦力がはたらいているので物体は動かない。ところが、Fがある大きさを超えたときから物体は動きだし、動摩擦力f'(=μ'N)がはたらくことになる。この物体が動き出す直前の静止摩擦力f0のことを最大摩擦力(最大静止摩擦力)という。最大摩擦力は静止摩擦力なので、もちろん力のつり合いの関係が成り立っているが、特別に次の公式で求めることもできる。垂直抗力をN[N]として、
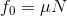
このときのμを静止摩擦係数という。
