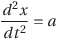微分積分
物理ではグラフを扱うことが非常に多く、さらにその傾きや"面積"まで考えなくてはならない。今回はグラフの傾きについて詳しく見ていこう。これまでに紹介したグラフとその傾きの関係は以下の通り。
- x-tグラフの傾きは速度vを表す。
- v-tグラフの傾きは加速度aを表す。
平均変化率
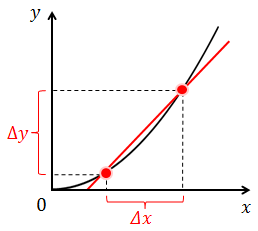
y-xグラフ上の2点間を結ぶ直線の傾きは、xの変化量をΔx,yの変化量をΔyとすると、
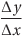
で表すことができる。これを平均変化率という。もちろん、x-tグラフやv-tグラフの場合には
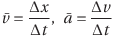
と表現され、これらは平均の速度、平均の加速度を表していることが分かる。
- vやaの上の「-」は、平均値であることを強調するときに用いる。
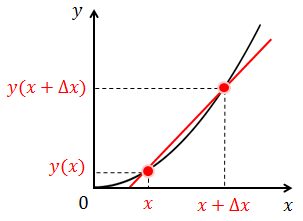
また、x=xのときのyの値をy(x)と書くことにすると、xの値がxからx+Δxへ変化したときの平均変化率は、
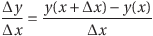
と表すこともできる。
微分
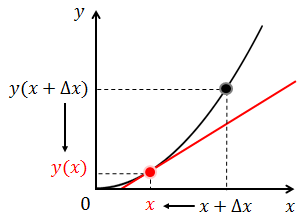
次は、グラフ上の1点(x,y)で接する直線(接線)を考えよう。Δxを小さくしていくと、グラフ上の2点を結ぶ直線も徐々に変化していく。そしてΔxがほぼ0となったときが(x,y)における接線である。この接線の傾きを微分係数といい、次のように表す。
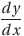
特に、x-tグラフやv-tグラフの微分係数は、瞬間的な変位や速度の変化を示すので、微分係数は瞬間の速度や瞬間の加速度を表しているといえる。
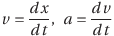
また、微分係数はΔxを限りなく0に近づけたときの平均変化率ということなので、これを
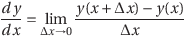
と表現する。一般的に、微分係数を表す関数を導関数と呼び、導関数を求めることを「微分する」という。
練習
(1) y=3x2
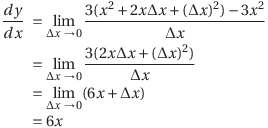
(2) y=2x
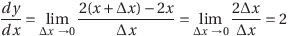
(3) y=2
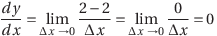
(4) y=3x2+2x+2
この微分の結果は、(1)~(3)の結果の和になっている。
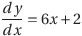
最後に、等加速度直線運動の式をtで微分してみよう。v0が定数であることに注意して、
・速度の式をtで微分
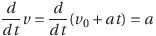
・変位の式をtで微分
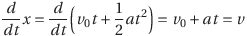
積分
関数y(x)の導関数y'(x)を求めることを「微分する」といった。
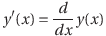
また、微分するとy(x)になるような関数Y(x)をy(x)の原始関数と呼び、y(x)からY(x)を求めることを「積分する」という。積分の計算は次のように表現する。
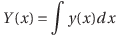
ところで、速度v(t)をtで微分すると加速度aになるのだった。
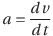
それでは、加速度a(定数)をtで積分して等加速度直線運動の速度の式v(t)を求めてみよう。まずは、上の式を
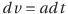
と変形して、積分記号を付ける。
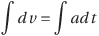
左辺はdvの前に1が隠れていると考えるので、vで微分して1になるような関数を探せばいい。その条件には、「v」もしくはそれに定数を加えた「v+1」「v+2」「v+3」などが当てはまる。そこで、定数C1を使って、
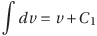
と表すことにしよう。C1を積分定数という。また、定数C2を使って同じように考えると、右辺は
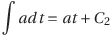
と表せるから、元の式は
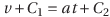
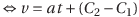
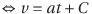
になる。C(=C2-C1)は新しい積分定数。
ここで、初期条件を考えてCを決めよう。時刻t=0における速度(初速度)をv=v0とすると、
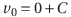
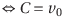
である。よって、
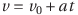
続いて等加速度直線運動の変位の式を導こう。変位x(t)をtで微分すると速度v(t)になるという内容からスタートする。
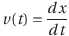
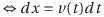
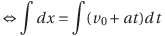
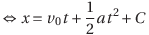
Cは積分定数。ここで時刻t=0における変位をx=0とすると、
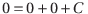
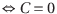
になるから、
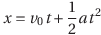
- ところで、「xをtで2回微分するとaになる」という内容を次のように表す。