力と運動

力学的エネルギー保存則 ←→ 等速円運動

　微分してf(x)になるような関数F(x)(原始関数)を求めることを積分といった。これとは別に、範囲を決めてグラフの面積を求めることも積分という。これらを区別するために、前者を不定積分、後者を定積分と呼ぶことにしよう。

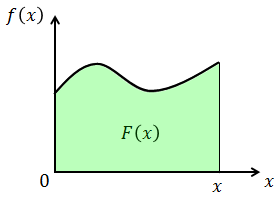
　ある関数f(x)の不定積分を

と書いたとき、f(x)のグラフの面積は、F(x)に等しい。

　だから、ｘ=a~bの範囲のグラフの面積Sを考えてみると、F(b)とF(a)の差になっていることが分かる。

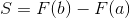
これは関数F(x)にaとbを代入して引き算するということなので、この計算を

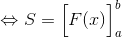
と表そう。また、今はx=a～bの範囲にしぼってf(x)を積分するということだから、これを

と表すことにする。このような積分を定積分という。ただ、式を立ててから結果を求めるまでの流れは今の逆で、

になる。

練習

 f(x)=2x+3を、x=2~5の範囲で積分せよ。

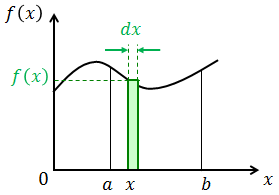
　定積分の計算の仕方は分かってもらえただろうか。次は定積分の式の意味を考えてみよう。いま、高さf(x)、幅dxの長方形の面積を計算すれば、

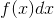
になる(上図)。ここでx=a~bの範囲のグラフの面積は、いま求めた細長い長方形の面積をx=a~bの範囲で足し合わせることで求められる。この内容を積分記号を用いて

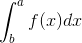
と表現する。

　今後、物理では何度も定積分のお世話になるので、簡単なイメージを紹介しておこう。まず、dxやdtのように頭にdが付いているものはxやtの微小変化量を表す。そしてこの微小量をa~bの範囲で足し合わせることを「定積分する」というのだ。

　例えば、東京から大阪までの距離s[m]を測るために、長さds [m]のものさしを用意したとすれば、あとはこのds[m]という長さを東京から大阪までひたすら足していけばいい。これを、

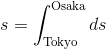
と書いたりするわけ。dのついた物理量と、∫の意味はなんとなくでもイメージできただろうか。特に∫の方は、ただの足し算だと思えば抵抗感も小さくなるのではないだろうか。

　f(x)=1/xのグラフをx>0の範囲で考える。このグラフは、xがどんどん大きくなるにしたがって0に近づいていく。この内容は

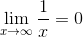
と書くことができる。このように、グラフがある1点に定まっていくことを「収束する」といい、このときの結果を極限という。

　また、今度はxをどんどん0に近づけていく。すると、このグラフは際限なく大きくなってしまう。この内容を

と書く。このように、いつまでもグラフが1点に定まらないことを「発散する」という。このときの極限は∞だといえる。ところで、sinｘやcosｘをx→∞に飛ばしたときもこの値は1点に定まらないが、この場合は特に「振動する」という。

練習

・f(x)=(2x+1)/x について、x→∞のときの極限を求めよ。

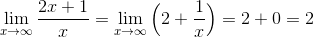
・f(θ)=sinθ/θについて、θ→0のときの極限を求めよ。

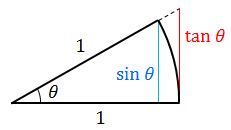
→半径1の円弧の長さは、弧度法を使うとθである。

• 弧度法は、半径1の円弧の長さをそのまま角度として採用したもの。詳しくは「等速円運動」で説明する。

　上の図より、θとsinθとtanθのあいだには、

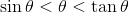
という大小関係が成り立っていることが分かる。次に、tanθ=sinθ/cosθであることに注意して全体をsinθで割って、

分母と分子を入れ替える。

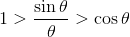
θ→0のとき、cosθ→1であるから、このときsinθ/θは1と1の間にはさまれていることになる。よって、明らかに

である。

　いま導いた関係を使うと、sinθやcosθの微分をすることができる。そこでまずはsinθを微分してみよう。微分の定義より、

分子を加法定理で変形すると、

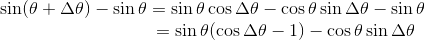
ここで、

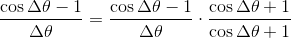
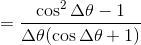
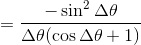
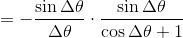
だから、この値はΔθ→0のとき

であることが分かる。ただし、

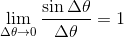
を利用した。以上より、

　続いてcosθの微分をしてみよう。微分の定義より、

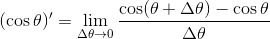
分子を加法定理を用いて変形すると、

よって、

と計算することができる。

　まとめると、

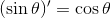
これから何度も出会うことになるので、覚えておくと便利。